A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
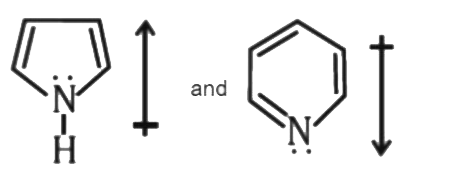
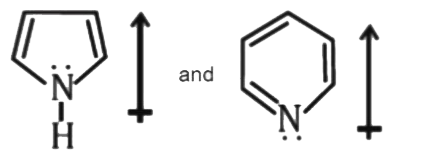
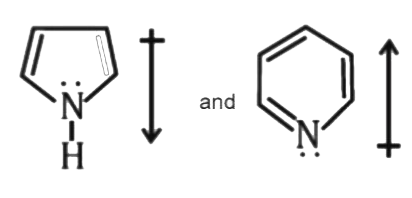
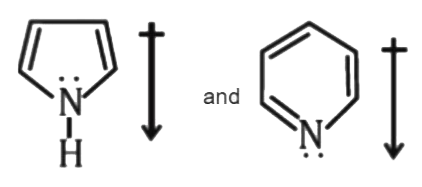
- The correct orientation of dipoles in pyrrole and pyridine is
Text Solution
|
- The hybridization states of the nitrogen atom in pyridine piperidine a...
Text Solution
|
- Pyridine is more basic than pyrrole. Which of these of following state...
Text Solution
|
- The hybridization states of the nitrogen atom in pyridine, piperdine a...
Text Solution
|
- (A) Pyrrole is more basic than pyridine. (R) In pyrrole, nitrogen is s...
Text Solution
|
- The only correct combination for pyrrole is
Text Solution
|
- Statement 1: Pyridine is mre basic than pyrrole. and Statement 2: ...
Text Solution
|
- Assertion: Pyrrole is more basic than pyridine. Reason: In pyrrole, ni...
Text Solution
|
- The hybridization states of the nitrogen in pyridine, piperidine and p...
Text Solution
|