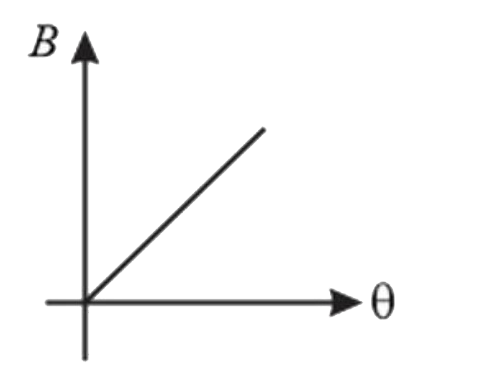
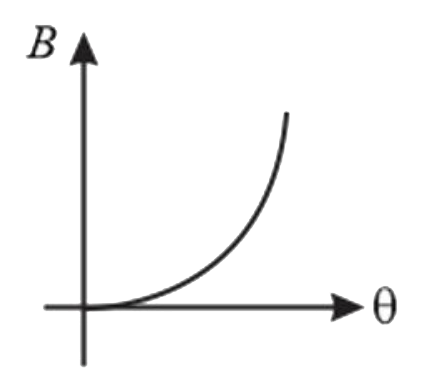
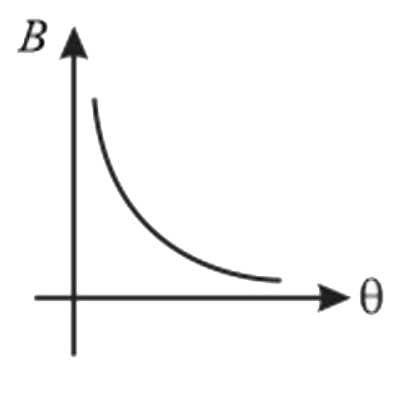
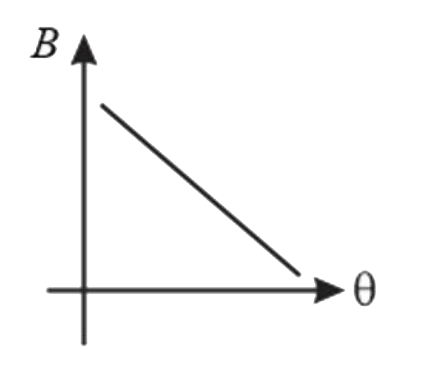
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A current - carrying wire of certain length is bent to form an arc tha...
Text Solution
|
- A wire of length l is bent in the form of an equilateral triangle and ...
Text Solution
|
- A piece of wire carrying a current of 6.00 A is bent in the form of a ...
Text Solution
|
- Two wires A and B have the same length equal to 44cm. and carry a curr...
Text Solution
|
- A wire of length 10cm is bent into an arc of a circle such that it sub...
Text Solution
|
- A long wire carrying a steady current is bent into a single coil such ...
Text Solution
|
- A current - carrying wire of certain length is bent to form an arc tha...
Text Solution
|
- A wire A , bent in the shape of an arc of a circle , carrying current ...
Text Solution
|
- A 0.5 m long conducting wire is bent in form of a circle, Calculate th...
Text Solution
|