A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
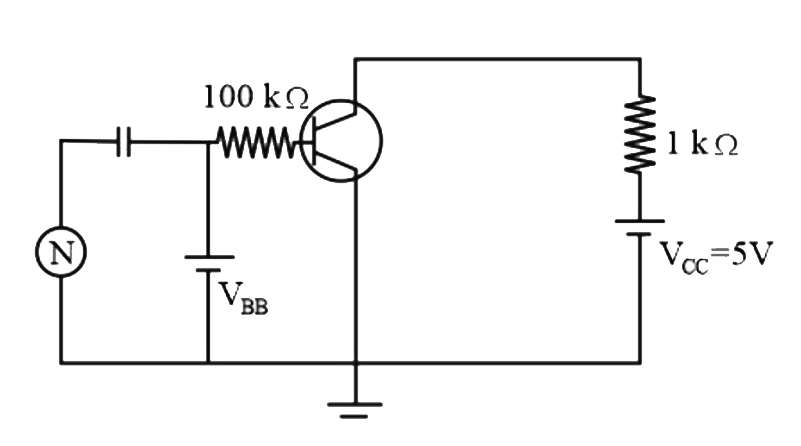
- V("BB") can vary between 0 and 5 V. Find the minimum value of base cur...
Text Solution
|
- In common emitter transistor as shown in Fig., the V(BB) supply can be...
Text Solution
|
- The output characterstics of an n-p-n transistor represent, [I(C) = Co...
Text Solution
|
- In the figure, given that V(BB) supply can vary from 0 to 5.0V,V(CC)=5...
Text Solution
|
- In the figure, given that V(BB) supply can vary from 0 to 5.0V,V(CC)=5...
Text Solution
|
- In the given figure, a transistor is connected in common emitter confi...
Text Solution
|
- चित्र में विघुत आपूर्ति V(BB) में 0 V से 5.0 V तक परिवर्तन किया जा सकत...
Text Solution
|
- The output characteristics of an n-p-n transistor represent, ( I(C) = ...
Text Solution
|
- V("BB") can vary between 0 and 5 V. Find the minimum value of base cur...
Text Solution
|