Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
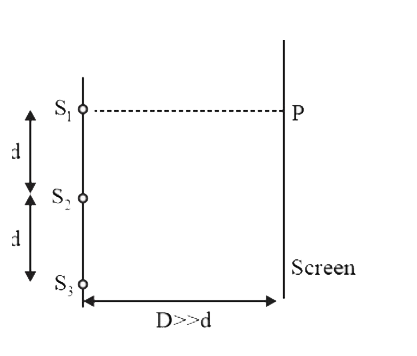
- Consider the interference at P between waves emitting from three coher...
Text Solution
|
- Three sources of sound S(1),S(2) and S(3) of equal intensity are place...
Text Solution
|
- A monochromatic light source of wavelength lamda is placed at S. three...
Text Solution
|
- Three coherent sources S(1), S(2)" and" S(3) can throw light on a scre...
Text Solution
|
- In the case of light waves from two coherent sources S(1) and S(2) , t...
Text Solution
|
- In the figure shown S(1)O-S(2)O=S(3)O-S(2)O=(lambda)/(4) , Intensity a...
Text Solution
|
- धवनि की तीन स्त्रोत S(1), S(2) तथा एS(3) क ही रेखा में रखे हुए है ...
Text Solution
|
- S(1) and S(2) are two coherent sources. The intensity of both sources ...
Text Solution
|
- Two sound waves each of wavelength lamda and having the same amplitude...
Text Solution
|