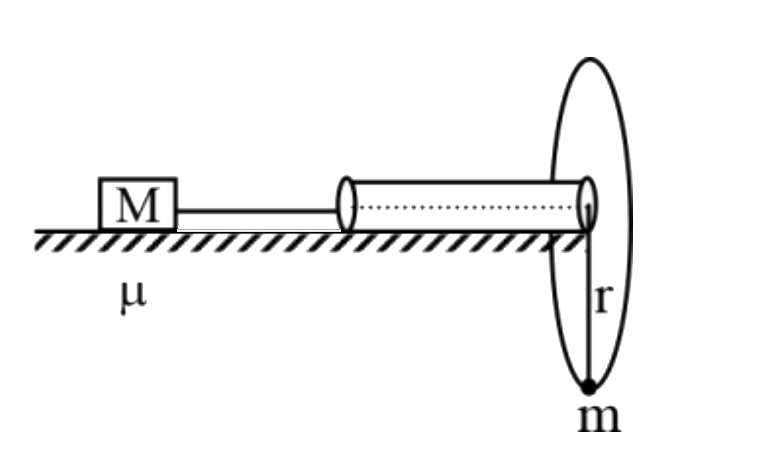
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The figure below shows a block of mass M connected to an ideal string ...
Text Solution
|
- Figure shown a block of mass m placed on a smooth wedge of mass M. Cal...
Text Solution
|
- A block of mass m is stationary on a horizontal surface. It is connect...
Text Solution
|
- A toy car of mass m can travel at a fixed speed. It moves in circle on...
Text Solution
|
- In the arrangement shown in figure , there is friction between the bl...
Text Solution
|
- Coefficient of friction between block of mass m and fixed wedge is mu ...
Text Solution
|
- A block of mass M is placed on a horizontal surface. It is tied with a...
Text Solution
|
- A block of mass M is placed on a rough horizontal surface. It is conne...
Text Solution
|
- A block of mass M is placed on a rough horizontal surface. It is conn...
Text Solution
|