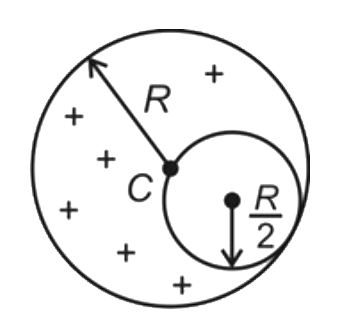
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A non - conducting disc of radius R is uniformly charged with surface ...
Text Solution
|
- Charge q is uniformly distributed on a disc of radius r. If the disc i...
Text Solution
|
- Find the potential varphi at the edge of a thin disc of radius R carry...
Text Solution
|
- A non-conducting thin disc of radius R and mass m having charge unifor...
Text Solution
|
- A non-conducting semi circular disc (as shown in figure) has a uniform...
Text Solution
|
- The surface charge density of a thin charged disc of radius R is sigma...
Text Solution
|
- A uniform disc of radius R is charged with a uniform surface charge de...
Text Solution
|
- A flat disc of radius R charged uniformly on its surface at a surface ...
Text Solution
|
- Figure-4.11 shows a circular a disc of radius R from which a small dis...
Text Solution
|