Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
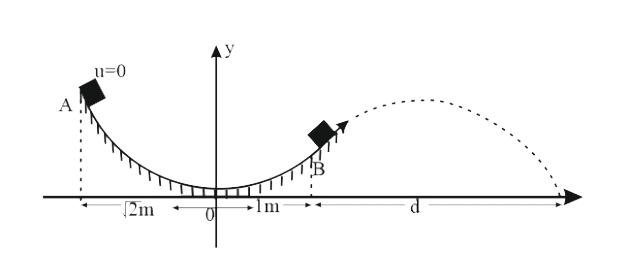
- A small body is released from point A of smooth parabolic path y=x^(2)...
Text Solution
|
- In the figure shown all the surface are smooth. All the blocks A,B and...
Text Solution
|
- A body of mass (m) is projected with a speed (v) making an angle theta...
Text Solution
|
- A wedge as shown in figure has a rough curved surface of coefficient o...
Text Solution
|
- The path followed by a body projected along y axis is given by y=sqrt(...
Text Solution
|
- In the figure shown all the surface are smooth. All the blocks A, B an...
Text Solution
|
- A body is projected horizontally from a point above the ground. The mo...
Text Solution
|
- A small body is released from point A of smooth parabolic path y=x^(2)...
Text Solution
|
- A body is projected with a velocity of 60 m/s at 30^(@) to horizontal ...
Text Solution
|