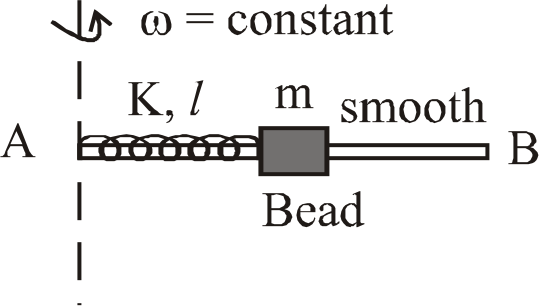A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- AB is a light rigid rod. Which is rotating about a vertical axis passi...
Text Solution
|
- AB is a light rigid rod. Which is rotating about a vertical axis passi...
Text Solution
|
- A rigid mass less rod of length L is rotating in a vertical plane abou...
Text Solution
|
- AB is a light rigid rod. Which is rotating about a vertical axis passi...
Text Solution
|
- A bead of mass m can slide without friction on a fixed circular horizo...
Text Solution
|
- A bead of mass m can slide without friction along a vertical ring of r...
Text Solution
|
- A long horizontal rod has a bead which can slide along its length, and...
Text Solution
|
- An underformed spring of spring constant k is connected to a bead of m...
Text Solution
|
- A smooth uniform rod of length L and mass M has two identical beads of...
Text Solution
|