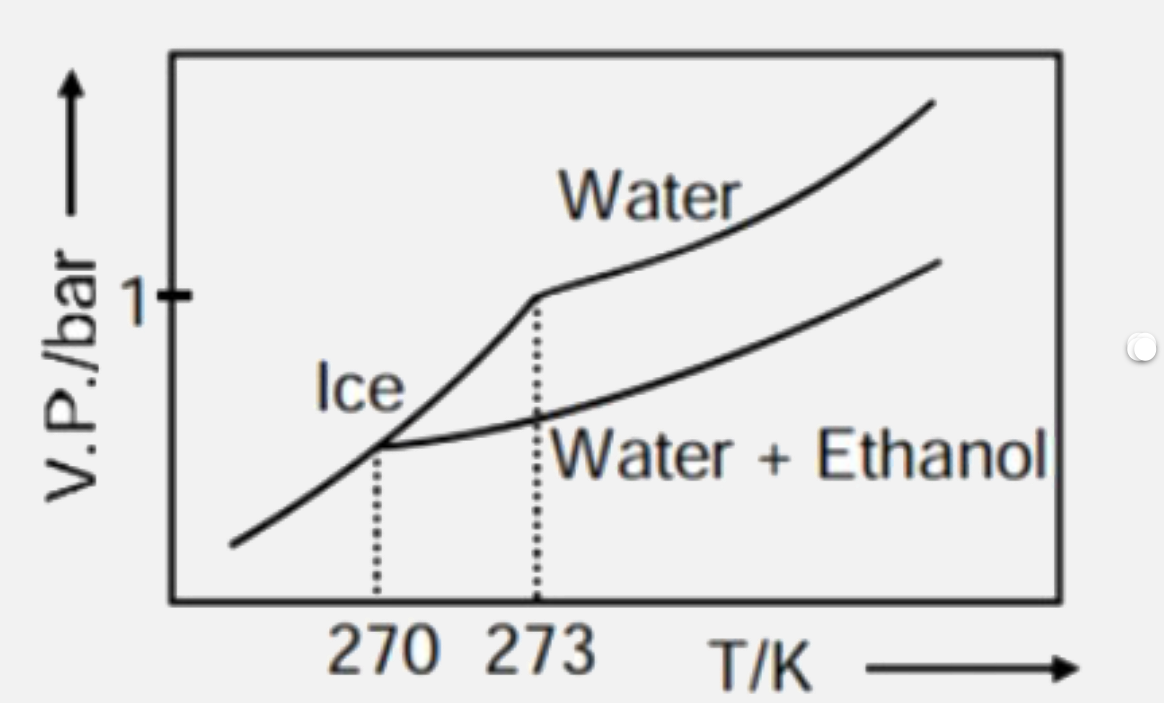
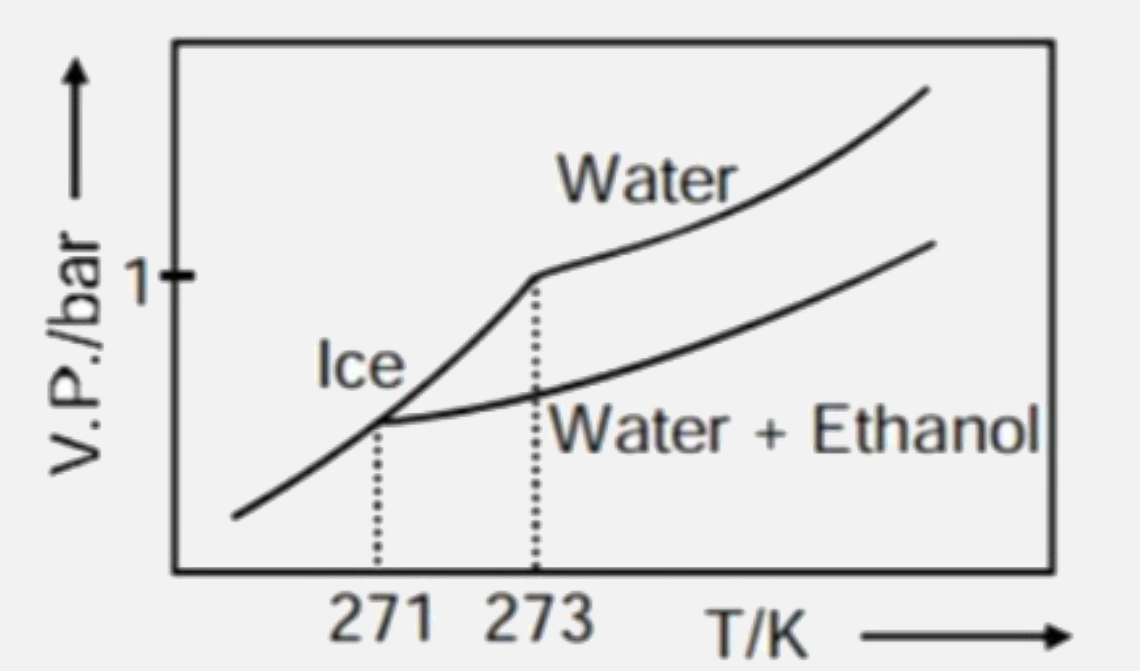
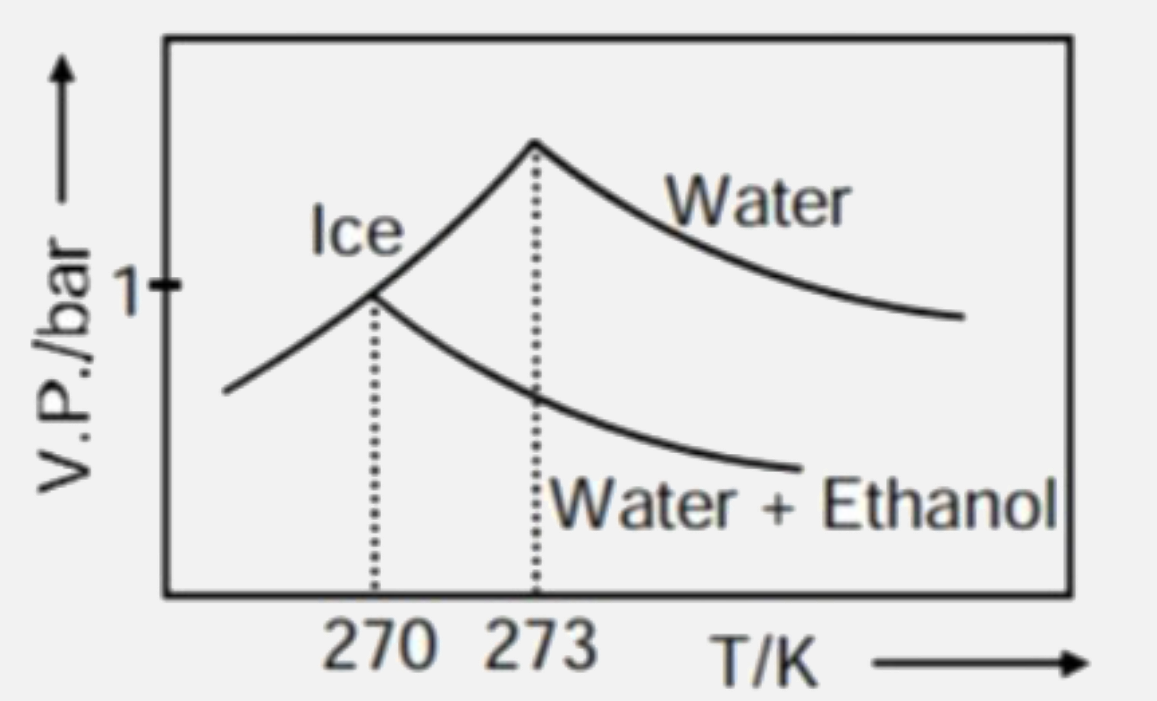
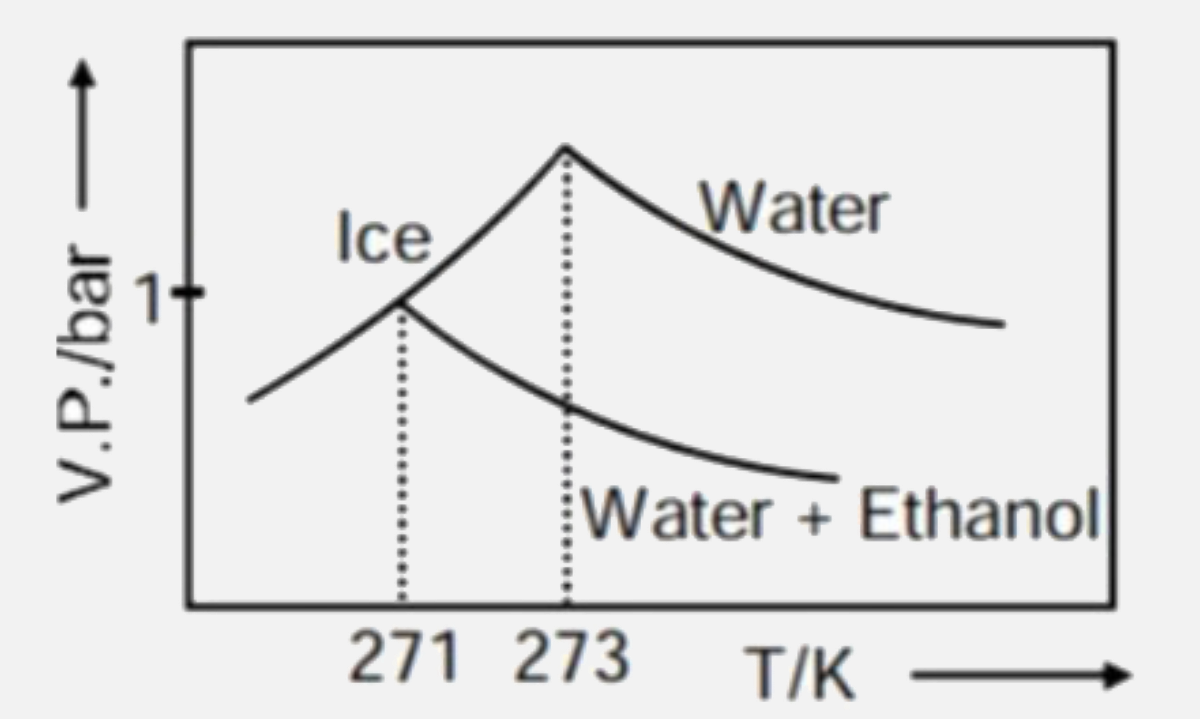
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Pure water freezes at 273 K and 1 bar. The addition of 34.5 g of ethan...
Text Solution
|
- A solution M is prepared by mixing ethanol and water. The mole fractio...
Text Solution
|
- A solution M is prepared by mixing ethanol and water. The mole fractio...
Text Solution
|
- A solution M is prepared by mixing ethanol and water. The mole fractio...
Text Solution
|
- Pure water freezes at 273 K and 1 bar. The addition of 34.5 g of ethan...
Text Solution
|
- Pure water freezes at 273 K and 1 bar. The addition of 34.5 g of ethan...
Text Solution
|
- Pure water freezes at 273 K and 1 bar. The addition of 34.5 g of ethan...
Text Solution
|
- Pure water freezes at 273 K and 1 bar. The addition of 34.5 g of ethan...
Text Solution
|
- Properties such as boiling point, freezing point and vapour, pressure ...
Text Solution
|