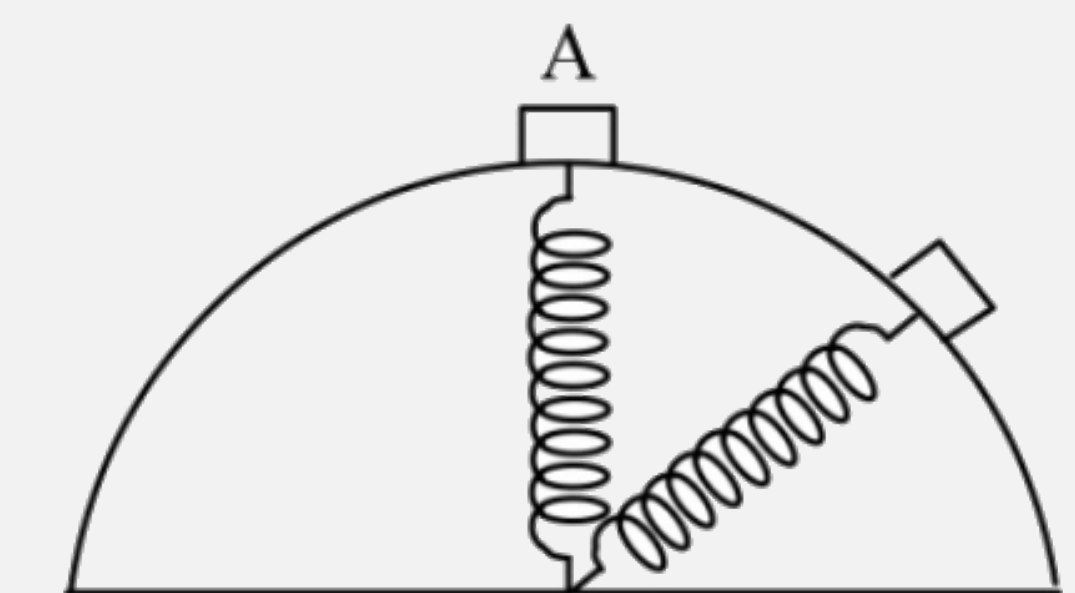
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A bead of mass m can slide without friction along a vertical ring of r...
Text Solution
|
- A ring of mass M hangs from a thread and two beads of mass m slides on...
Text Solution
|
- Four beads each of mass m are glued at the top, bottom and the ends of...
Text Solution
|
- A Bead of mass m is attached to one end of a spring of natural length ...
Text Solution
|
- A bead of mass m is threaded on a smooth circular wire centre O, radiu...
Text Solution
|
- A bead of mass m is threaded on a smooth circular wire centre O, radiu...
Text Solution
|
- A bead of mass m is threaded on a smooth circular wire centre O, radiu...
Text Solution
|
- A ring of radius R lies in vertical plane. A bead of mass 'm' can move...
Text Solution
|
- A massless ring hangs from a thread and two beads of mass m slide it w...
Text Solution
|