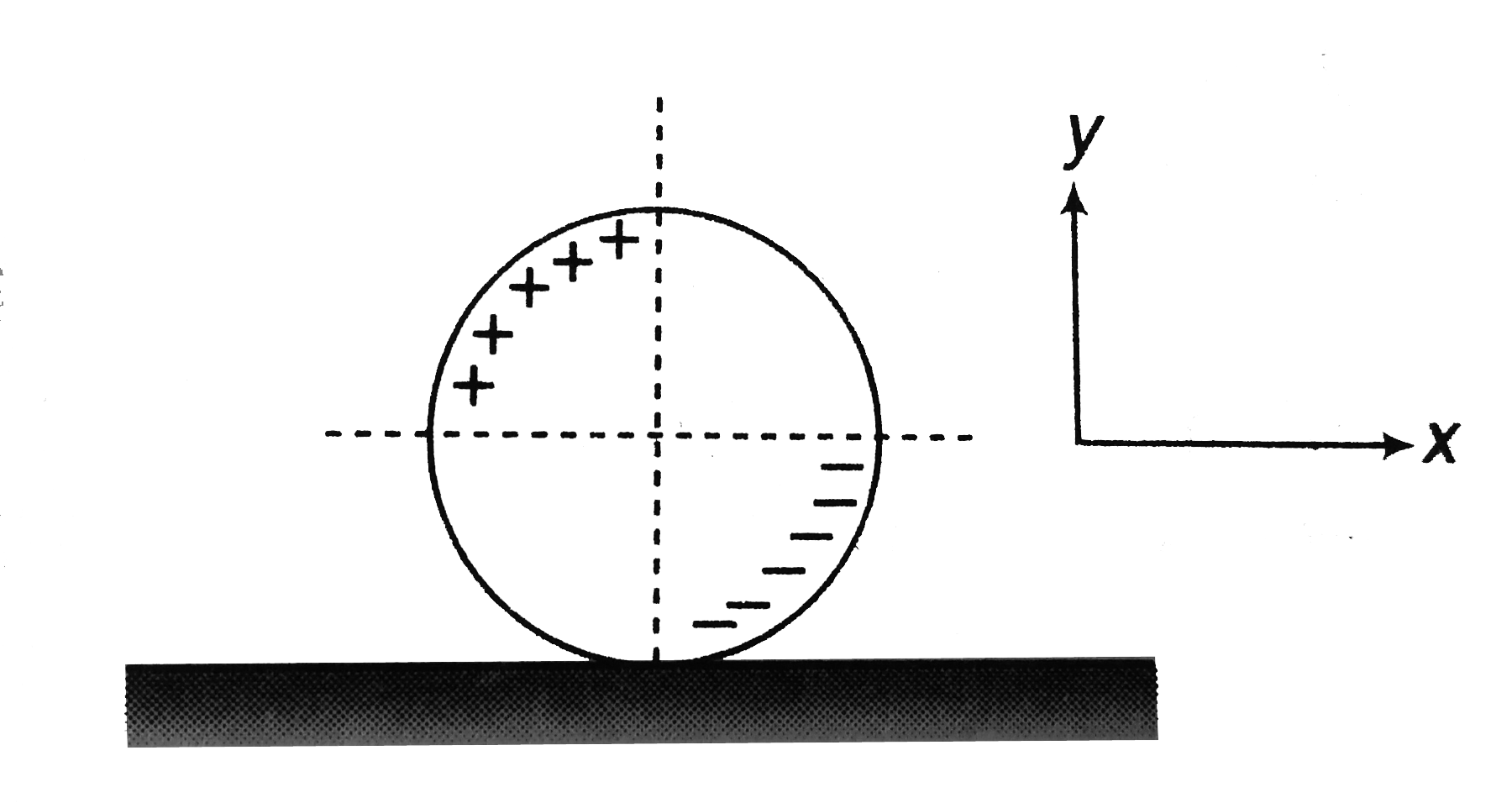A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A non-conducting ring of mass m and radius R is charged as shown. The ...
Text Solution
|
- A nonconducting ring of mass m and radius R, with charge per unit leng...
Text Solution
|
- A non conducting solid sphere of mass m and radius R having uniform ch...
Text Solution
|
- A non conducting ring of radius R is charged as shown in figure : Figu...
Text Solution
|
- A non-conducting ring of radius r has charge per unit length lambda. A...
Text Solution
|
- A half ring of radius R has a charge of lambda per unit length. The el...
Text Solution
|
- A thin conducting ring of radius R is given a charge +Q, Fig. The elec...
Text Solution
|
- A thin conducting ring of radius R is given a charge +Q. The electric ...
Text Solution
|
- A nonconducting ring of mass m and radius R is charged as shown. The c...
Text Solution
|