A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
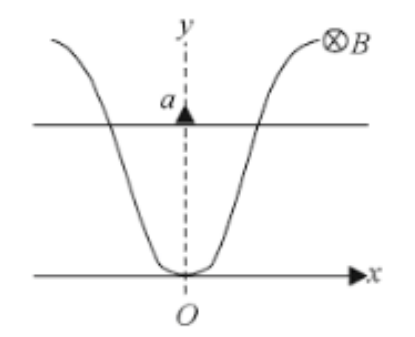
- A wire bent as a parabola y=kx^(2) is located in a uniform magnetic fi...
Text Solution
|
- A copper wire bent in the shape of a semicircle of radius r translates...
Text Solution
|
- A loop of wire enclosing an area S is placed in a region where the mag...
Text Solution
|
- A wire is bent in the form of a V shape and placed in a horizontal pl...
Text Solution
|
- A rectangular loop with a sliding conductor of length l is located in ...
Text Solution
|
- Consider the sliding wire circuit shown in . The wire slides at const...
Text Solution
|
- A wire bent as a parabola y=ax^(2) is located in a uniformed magnetic ...
Text Solution
|
- A wire loop enclosing a semi-circle of radius Ris located on the bound...
Text Solution
|
- A wire bent as a parabola y=kx^(2) is located in a uniform magnetic fi...
Text Solution
|