Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A non - conducting rod of length L with linear charge density lambda=l...
Text Solution
|
- A rod has a total charge Q uniformly distributed along its length L. I...
Text Solution
|
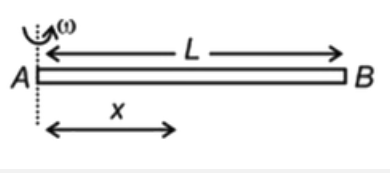
- A copper rod AB of length l is rotated about one end A with a constant...
Text Solution
|
- A horizontal rod AB of length 1 is rotated with constant angular veloc...
Text Solution
|
- When a rod of length l is rotated with angular velocity of omega in a ...
Text Solution
|
- A non–uniform thin rod of length L is placed along x-axis as such its ...
Text Solution
|
- A non - conducting rod of length L with linear charge density lambda=l...
Text Solution
|
- A uniform rod of length l rotating with an angular velocity omega , wh...
Text Solution
|
- A rod has a total charge Q uniformly distributed along its length L. I...
Text Solution
|