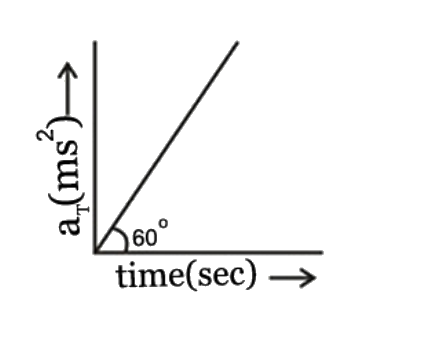
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Tangental acceleration of a particle moving in a circle of radius 1 m ...
Text Solution
|
- Initial velocity and acceleration of a particles are as shown in the ...
Text Solution
|
- Figure shows the total acceleration and velocity of a particle moving ...
Text Solution
|
- In a circular motion of a particle the tangential acceleration of the ...
Text Solution
|
- A particle is moving in a straight line. Particle was initially at res...
Text Solution
|
- The velocity -time (v - t) graph of a particle moving in a straight li...
Text Solution
|
- Tangental acceleration of a particle moving in a circle of radius 1 m ...
Text Solution
|
- In a circular motion of a particle , the tangential acceleration of th...
Text Solution
|
- In a circular motion of a particle , the tangential acceleration of th...
Text Solution
|