A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
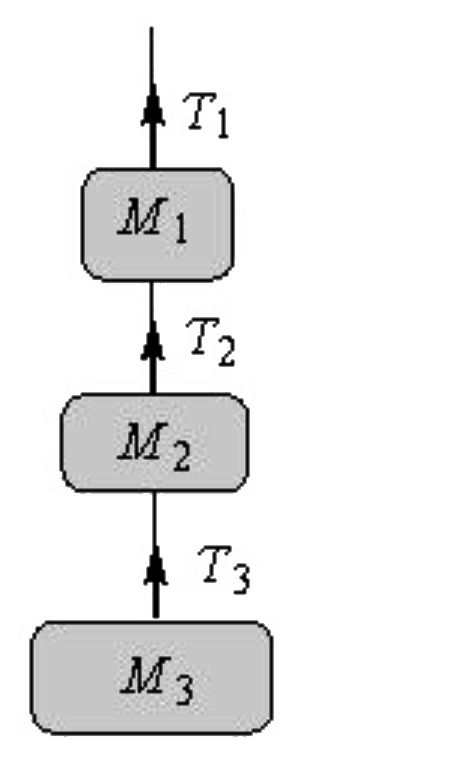
- The masses M(1), M(2) and M(3) are 5, 2 and 3 kg respectively. These h...
Text Solution
|
- The masses m(1) m(2) and m(3) of the three bodies shown in fig . Are 5...
Text Solution
|
- Two masses of 5 kg and 3 kg are suppended with help of massless inexte...
Text Solution
|
- Consider three blocks of masses m(1),m(2),m(3) interconnected by strin...
Text Solution
|
- Three blocks of masses m(1),m(2) and m(3) are connected by massless st...
Text Solution
|
- Two masses m(1) and m(2) are accelerated uniformly on a frictionless s...
Text Solution
|
- In the figure shown, m(1) = 10kg, m(2) = 6kg, m(3) = 4kg. If T(3) = 40...
Text Solution
|
- Two objects A and B of masses m(A) and m(B) are attached by strings as...
Text Solution
|
- The masses M(1), M(2) and M(3) are 5, 2 and 3 kg respectively. These h...
Text Solution
|