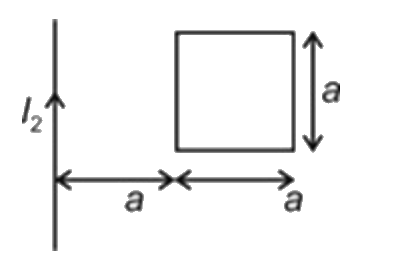
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- In the diagram shown, I(1), I(2) are the magnitudes of current in the ...
Text Solution
|
- A square loop ABCD , carrying a current I(2) is placed near and coplan...
Text Solution
|
- Circular loop of a wire and a long straight wire carry current I(c ) a...
Text Solution
|
- Two long parallel straight conductors carry current i(1) and i(2)(i(1)...
Text Solution
|
- An electric current i(1) can flow in either direction through loop-1 a...
Text Solution
|
- Assertion At the centre of a circular current carrying loop (I(1)), t...
Text Solution
|
- In the diagram I(1),I(2) are the strength of the currents in the loop ...
Text Solution
|
- A rectangular loop carrying a current i(2) situated near a long straig...
Text Solution
|
- Two circular loops A and B of radii R and 4R are kept concentrically i...
Text Solution
|