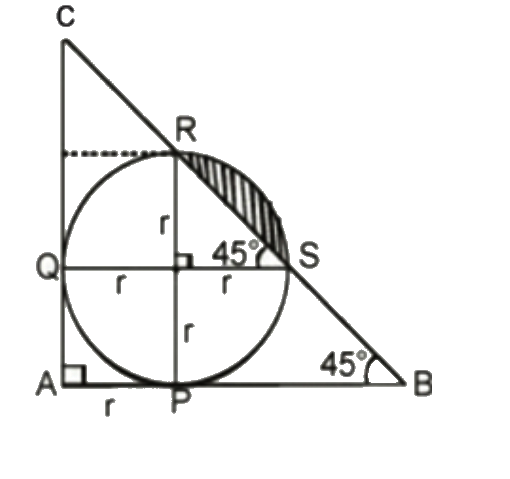
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- ABC is a right triangle, right - angled at the vertex A. A circle is d...
Text Solution
|
- The sides AB,BC and AC of a triangle ABC touch a circle with centre O ...
Text Solution
|
- एक समकोण त्रिभुज ABC में कोण B समकोण है | यदि भुजाओ AB और BC पर क्रमश:...
Text Solution
|
- ABC is a right triangle, right - angled at the vertex A. A circle is d...
Text Solution
|
- समकोण त्रिभुज ABC क़ि भुजा AB को व्यास मानकर खींचा गया वृत्त कर्ण AC को...
Text Solution
|
- In a right triangle ABC, a circle with a side. AB as diameter is draw...
Text Solution
|
- In a right triangle ABC, a circle with a side. AB as diameter is draw...
Text Solution
|
- Dileep started a business with a capital of Rs. 8000. After six months...
Text Solution
|
- In an isosceles right angle triangle ABC (at B) perpendicular are dra...
Text Solution
|