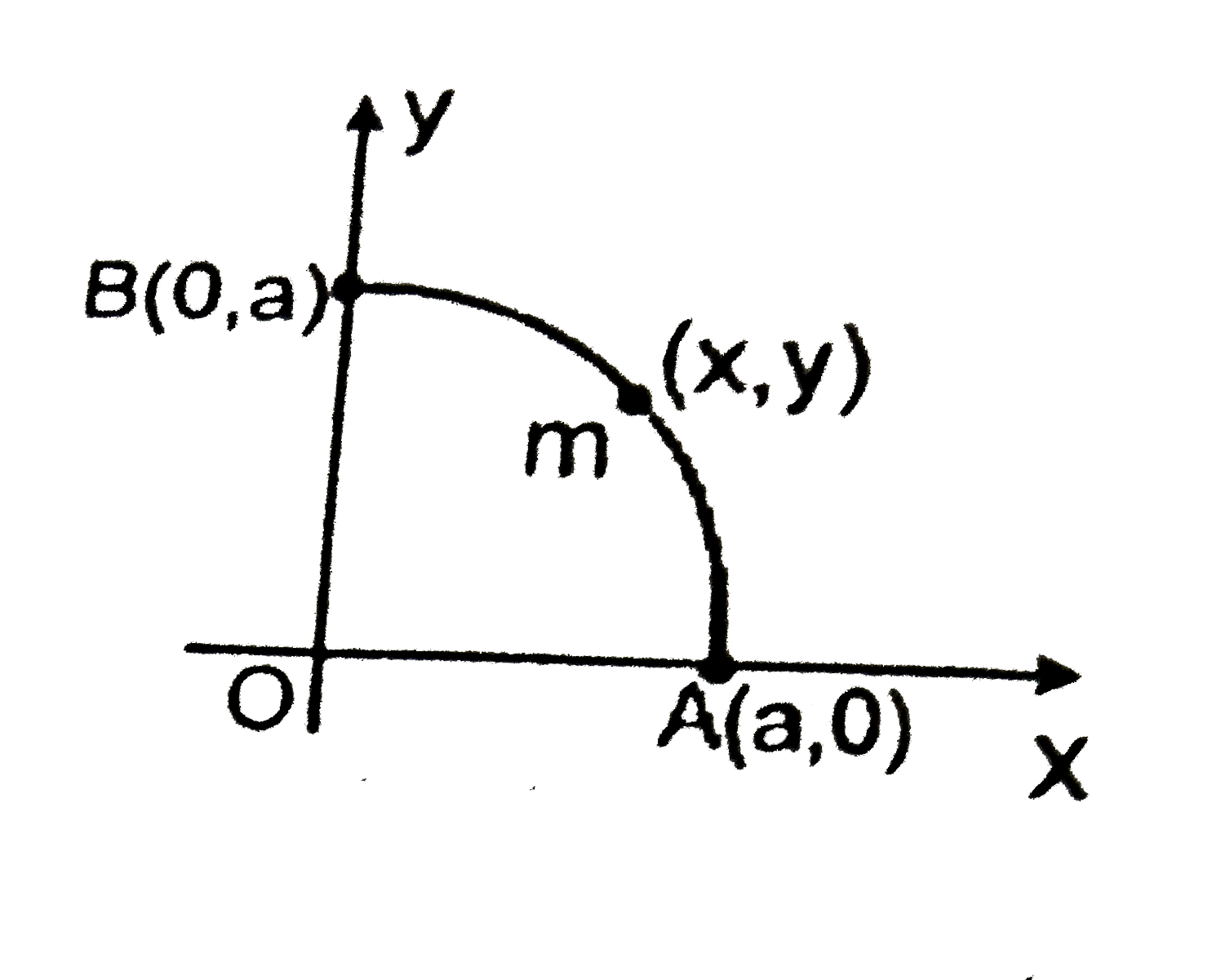A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle of mass 'm' moves along the quarter section of the circular...
Text Solution
|
- A particle of mass 'm' moves along the quarter section of the circular...
Text Solution
|
- द्रव्यमान का एक कण त्रिज्या के वृत्तीय पथ पर एकसमान चाल से गतिमान है...
Text Solution
|
- समान द्रव्यमान M वाले चार कण पारस्परिक गुरूत्वीय बल के प्रभाव ...
Text Solution
|
- A force F=-K(yhati+xhatj) (where K is a positive constant) acts on a p...
Text Solution
|
- द्रव्यमान m का एक कण, त्रिज्या r के वृत्त पर नियत चाल से चल रहा है। वृ...
Text Solution
|
- वृत्ताकार पथ में गतिमान कण पर अभिकेंद्रीय बल द्वारा किया गया कार्य श...
Text Solution
|
- Consider a force acting on a particle given as vec( F) = yhat( i ) + x...
Text Solution
|
- A particle moves along a circular path of radius 7 cm. Estimate the di...
Text Solution
|