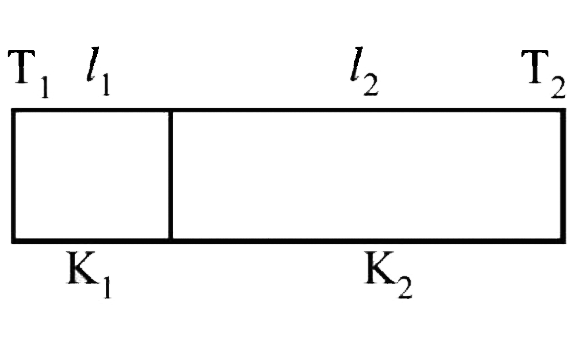
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- One end of a thermally insulated rod is kept at a temperature T1 and t...
Text Solution
|
- One end of a thermally insulated rod is kept at a temperature T1 and t...
Text Solution
|
- Two plates eachb of area A, thickness L1 and L2 thermal conductivities...
Text Solution
|
- Eleven identical rods are arranged as shown in Fig. Each rod has lengt...
Text Solution
|
- Two rods A and B have lengths l1 and l2. Each rod has its ends at temp...
Text Solution
|
- One end of thermally insulated rod is kept at a temperature T(1) and t...
Text Solution
|
- One end of a rod, enclosed in a thermally insulating sheath, is kept a...
Text Solution
|
- Two rods whose lengths are l1 and l2 and heat conductivity coefficient...
Text Solution
|
- Two rods of the same length and areas of cross-section A1 and A2 have ...
Text Solution
|