A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
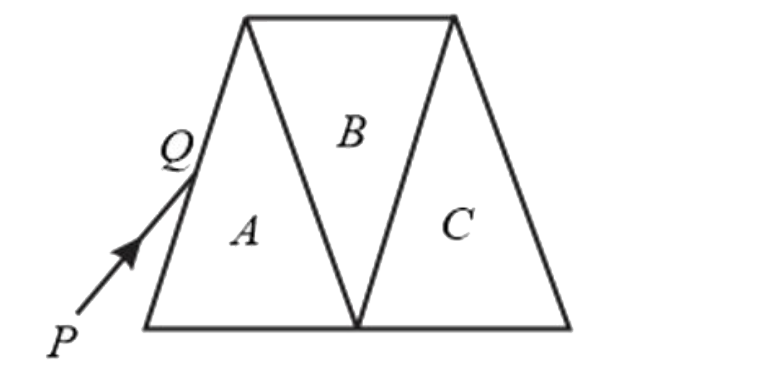
- The ray PQ shown in the figure , surface minimum deviation in an equil...
Text Solution
|
- A prism can produce a minmum deviation delta in a the beam. If three s...
Text Solution
|
- A given ray of light suffers minimum deviation in an equilateral prism...
Text Solution
|
- A given ray of light suffers minimum deviation in an equilateral prism...
Text Solution
|
- A prism can produce a minimum deviation delta in a light beam. If thre...
Text Solution
|
- An equilateral prism is placed on the prism table of a spectrometer in...
Text Solution
|
- A prism produces a minimum deviation § in a light beam. If three such ...
Text Solution
|
- A given ray of light suffers minimum deviation in an equilateral prism...
Text Solution
|
- A prism can produce a minmum deviation delta in a the beam. If three s...
Text Solution
|