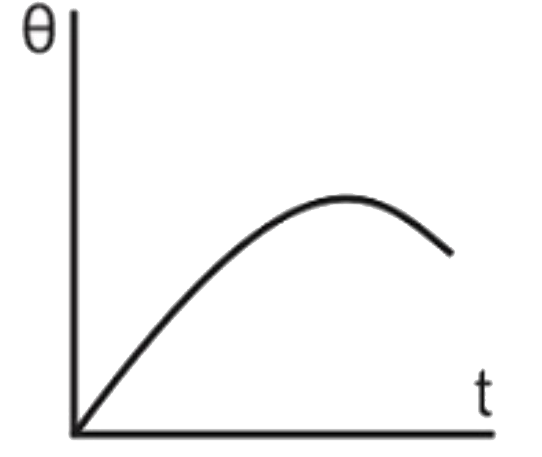
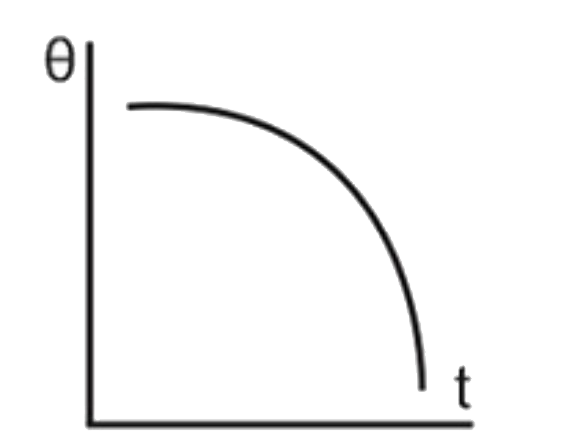
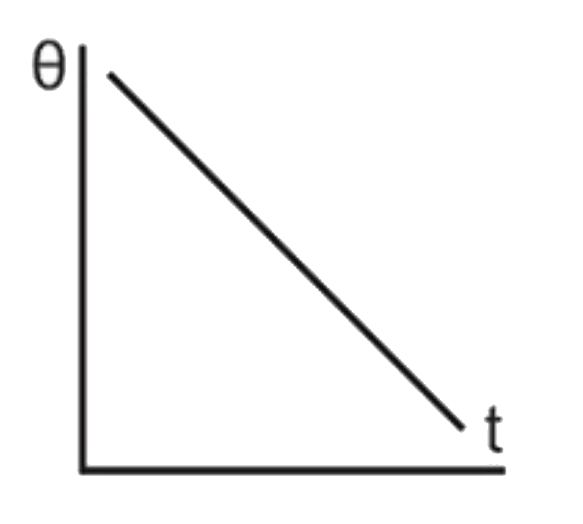
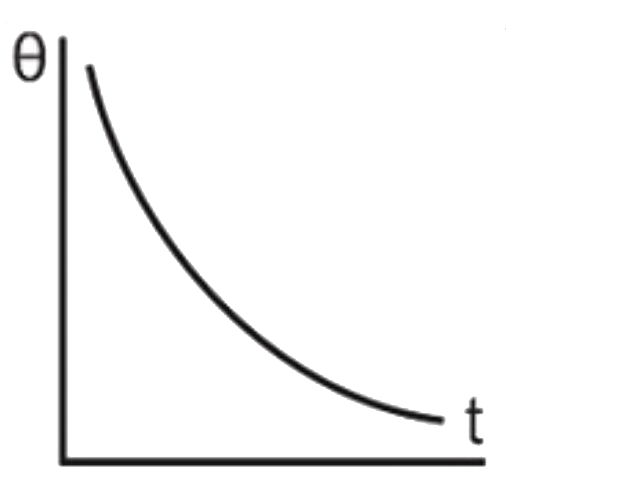
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The correct graph between the temperature of a hot body kept in cooler...
Text Solution
|
- A liquid in a beaker has temperature theta(t) at time t and theta0 is ...
Text Solution
|
- Newton's law of cooling holds good provided the temperature difference...
Text Solution
|
- एक बीकर में एक द्रव का ताप समय t पर theta है तथा वातावरण का ताप thet...
Text Solution
|
- Graph of rate of cooling against time is (assume Newton's law of cooli...
Text Solution
|
- State Newton's law of cooling and draw the graph showing cooling of ho...
Text Solution
|
- The excess temperature of a hot body above its surroundings is halved ...
Text Solution
|
- The correct graph between the temperature of a hot body kept in cooler...
Text Solution
|
- Instantaneous temperature difference between cooling body and the surr...
Text Solution
|