A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
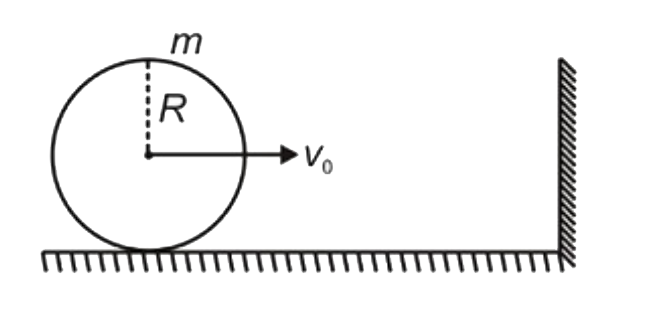
- A uniform solid sphere of mass m, radius R moving with velocity v0 is...
Text Solution
|
- A solid sphere of mass m and radius R is rolling without slipping as s...
Text Solution
|
- A sphere rolling on a horizontal rough surface Collides elastically wi...
Text Solution
|
- A sphere of mass M rolls without slipping on rough surface with centre...
Text Solution
|
- A sphere of mass m and radius r rolls without slipping on the horizont...
Text Solution
|
- A solid cylinder is rolling without slipping with velocity of its cent...
Text Solution
|
- A uniform solid sphere of mass m, radius R moving with velocity v0 is...
Text Solution
|
- The ratio of the acceleration for a solid sphere (mass m and radius R)...
Text Solution
|
- The ratio of the accelerations for a solid sphere (mass .m. and radius...
Text Solution
|