A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
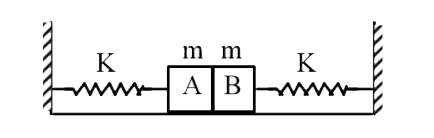
- Two blocks each of mass m are connected with springs each of force con...
Text Solution
|
- A block of mass m is attached to two unstretched springs of spring con...
Text Solution
|
- A block of mass m is connected to three springs as shown in Fig. The b...
Text Solution
|
- A small block is connected to a mass less rod, which is turn is attach...
Text Solution
|
- A particle of mass 'm' is attached to three identical springs A,B and ...
Text Solution
|
- The period of oscillation of a mass M suspended from a spring of sprin...
Text Solution
|
- चित्र 24.49 में प्रत्येक स्प्रिंग का बल नियतांक k है । प्रत्येक स्थि...
Text Solution
|
- Two blocks each of mass m are connected with springs each of force con...
Text Solution
|
- बल नियतांक K की एक स्प्रिंग व दो ब्लॉक क्रमशः m तथा M द्रव्यमान के , च...
Text Solution
|