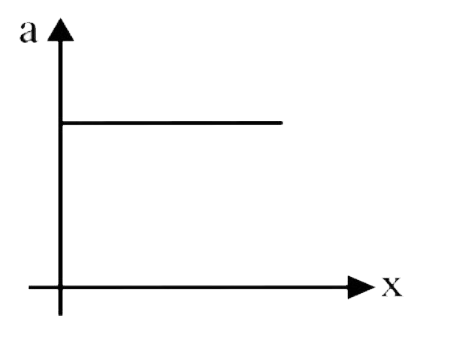
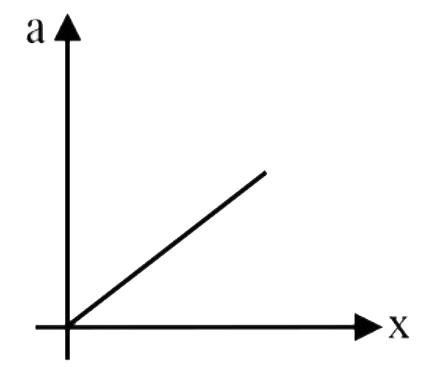
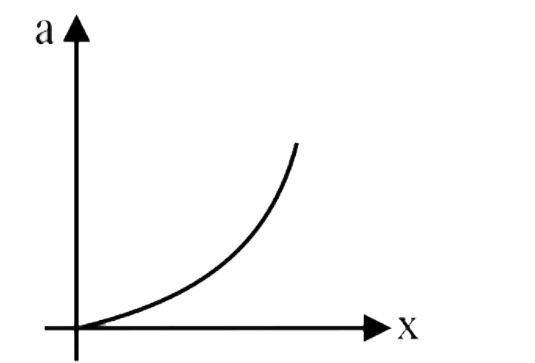
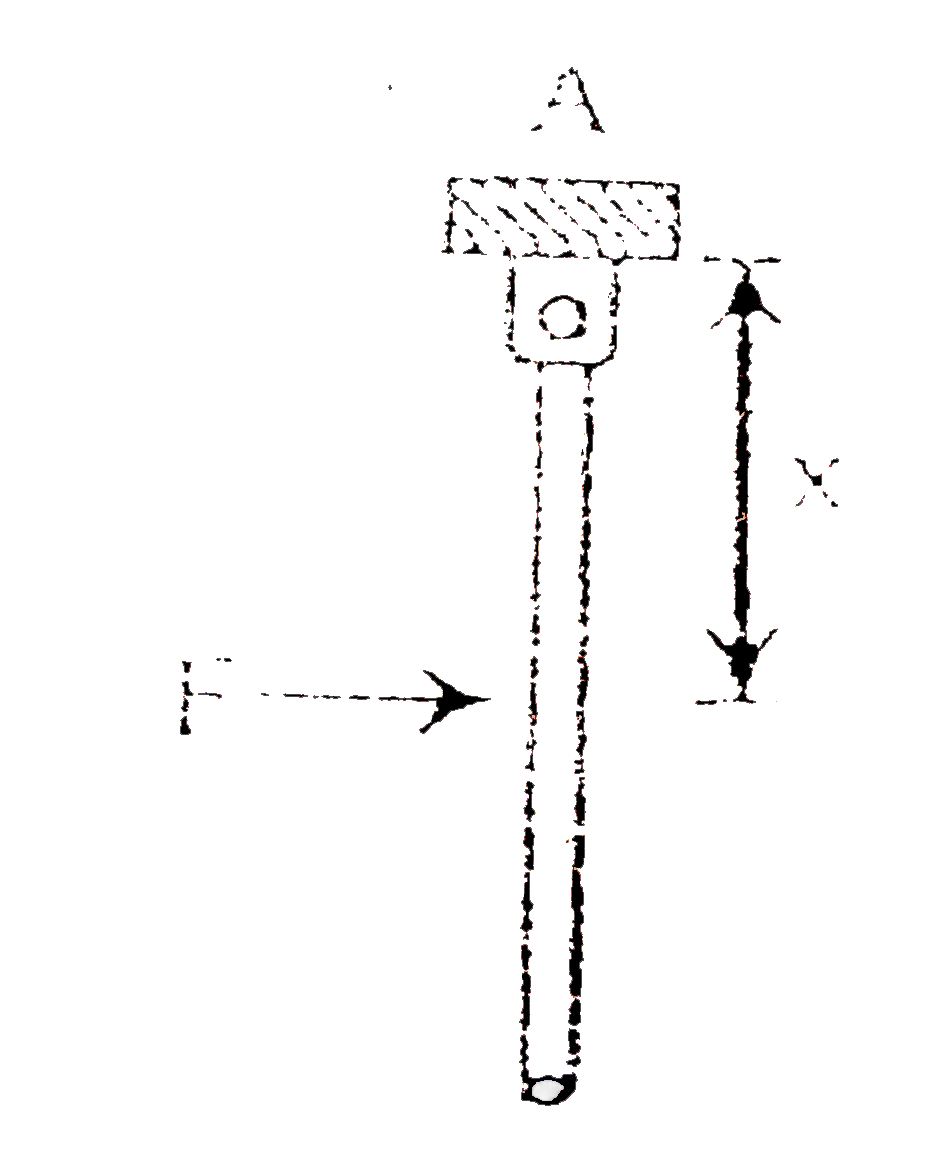A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A rod of mass m and length l is hinged at one of its ends A as shown i...
Text Solution
|
- One end of a uniform rod of length l and mass m is hinged at A. It is ...
Text Solution
|
- One end of a uniform rod of length l and mass m is hinged at A. It is ...
Text Solution
|
- A string of length L and mass M is lying on a horizontal table. A forc...
Text Solution
|
- A rod AB of mass M and length L is shown in figure. End A of rod is hi...
Text Solution
|
- A rod AB of mass M and length L is shown in figure. End A of rod is hi...
Text Solution
|
- The density of a rod of length L varies as rho=A+Bx where x is the dis...
Text Solution
|
- A rod of mass m and length L is hinged at its top end. If the rod is i...
Text Solution
|
- If the linear density of a rod of length L varies as lambda=(kx^(2))/(...
Text Solution
|