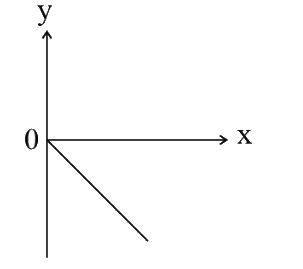
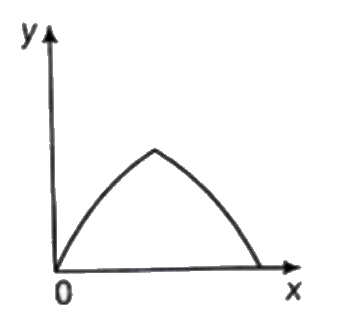
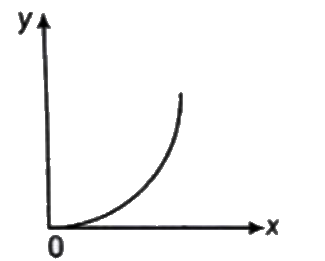
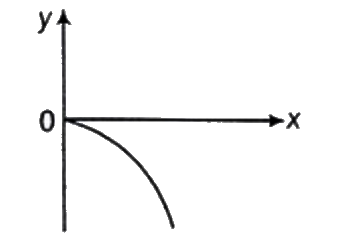
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two particles of mass m and 2m have their position vectors as a functi...
Text Solution
|
- A body of mass 1 kg begins to move under the action of a time dependen...
Text Solution
|
- Let r(1)(t)=3t hat(i)+4t^(2)hat(j) and r(2)(t)=4t^(2) hat(i)+3t^(2)hat...
Text Solution
|
- Find the shortest distance between the given line vec(r) =(3-t) hat(i...
Text Solution
|
- The position vector of a particle changes with time according to the r...
Text Solution
|
- The time dependence of the position of a particle of mass m = 2 is giv...
Text Solution
|
- किसी कण की स्थिति निम्न समीकरण द्वारा दी जाती है - vec(r ) = 3t ha...
Text Solution
|
- Two particles of mass m and 2m have their position vectors as a functi...
Text Solution
|
- Find the Cartesian equation of the following planes: (a) -> rdot( ha...
Text Solution
|