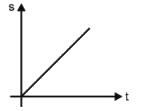
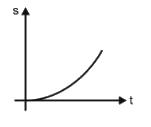
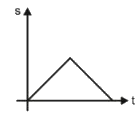
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- One stone is stored from a tower from rest and simultaneously another ...
Text Solution
|
- From a high tower, at time t=0, one stone is dropped from rest and sim...
Text Solution
|
- One stone is dropped from a tower from rest and simultaneously another...
Text Solution
|
- A stone is allowed to fall from the top of a tower 100m high and at th...
Text Solution
|
- A stone is dropped from the top of a tower 200 m high. At the same tim...
Text Solution
|
- A stone is dropped from the top of a 400 m high tower. At the same tim...
Text Solution
|
- From a high tower at time t=0, one stone is dropped from rest and simu...
Text Solution
|
- A stone is allowed to fall from a top of a tower 100 m high and at the...
Text Solution
|
- A stone is allowed to fall from a top of a tower 100 m high and at the...
Text Solution
|