A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
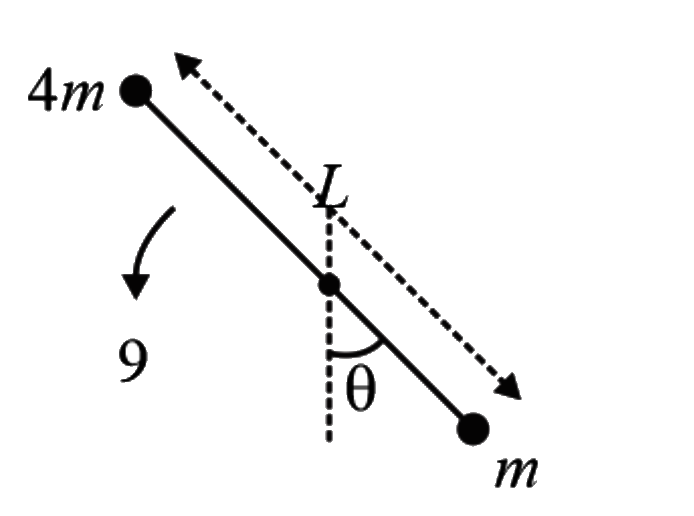
- Two balls of mass m and 4m are connected by a rod of length L. The mas...
Text Solution
|
- A uniform rod of mass 200 grams and length L = 1m is initially at rest...
Text Solution
|
- A small ball strikes a stationery uniform rod, which is free to rotate...
Text Solution
|
- A uniform rod of mass M and length L is hinged at its end to a wall so...
Text Solution
|
- A uniform rod of mass M and length L is hinged at its lower end on a t...
Text Solution
|
- There is an insulator rod of length L and of negligible mass with two ...
Text Solution
|
- Consider the situation shown in the figure. Uniform rod of length L ca...
Text Solution
|
- Two balls of mass m and 4m are connected by a rod of length L. The mas...
Text Solution
|
- A ball of mass m moving with a speed u(0) collides elastically with a ...
Text Solution
|