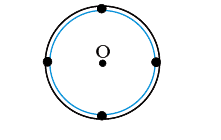
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Four similar point masses (each of mass m) are placed on the circumfer...
Text Solution
|
- A uniform disc of mass m and radius R has an additional rim of mass m ...
Text Solution
|
- The M.I. of disc of mass M and radius 'R' about an axis passing throug...
Text Solution
|
- Four similar point masses (m each) are symmetrically placed on the cir...
Text Solution
|
- Four particles, each of mass m, are lying symmetrically on the rim of ...
Text Solution
|
- The M.I. of a uniform semicircular disc of mass M and radius R about a...
Text Solution
|
- Out of a disc of mass M and radius R a concentric disc of mass m and r...
Text Solution
|
- A disc of radius r is removed from the centre of a disc of mass M and ...
Text Solution
|
- Four similar point masses (each of mass m) are placed on the circumfer...
Text Solution
|