A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
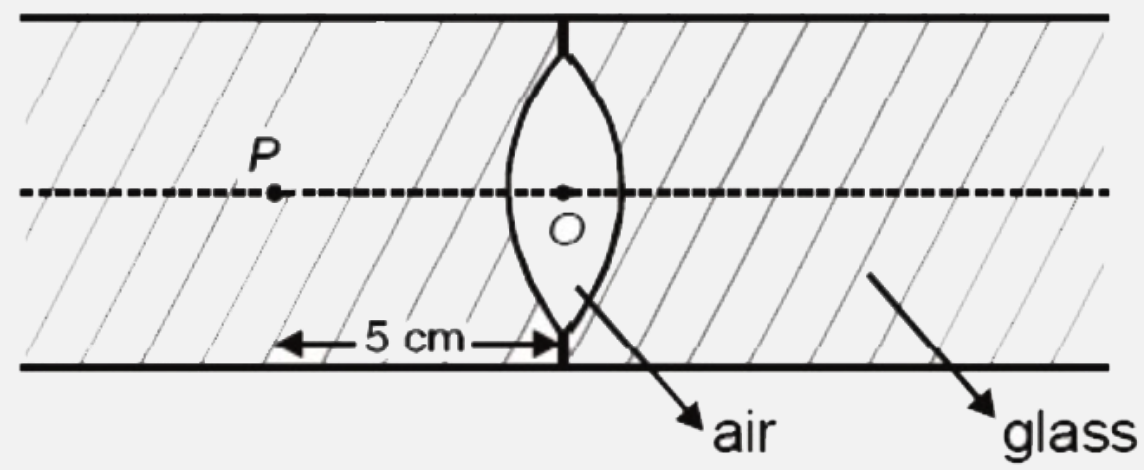
- Consider the show glass slab having a thin biconvex cavity of air cent...
Text Solution
|
- A spherical surface of radius of curvature R separates air (refractive...
Text Solution
|
- A spherical surface of radius of curvature R separates air (refractive...
Text Solution
|
- A biconvex thin lens is prepared from glass of refractive index mu(2)=...
Text Solution
|
- A glass slab of thickness 12 cm is placed on a table. The level surfac...
Text Solution
|
- Consider the show glass slab having a thin biconvex cavity of air cent...
Text Solution
|
- A spherical surface of radius of curvature R, separates air (refractiv...
Text Solution
|
- A thin biconvex lens is prepared from glass of refractive index mu(2)=...
Text Solution
|
- A biconvex thin lens prepared from glass of refractive index mu(2)=3/2...
Text Solution
|