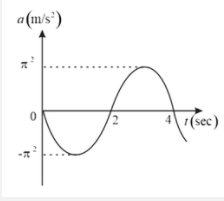
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A block performs simple harmonic motion with equilibrium point x = 0 ....
Text Solution
|
- A 100 g block is connected to a horizontal massless spring of force co...
Text Solution
|
- A 100 g block is connected to a horizontal massless spring of force co...
Text Solution
|
- A 100 g block is connected to a horizontal massless spring of force co...
Text Solution
|
- A 100 g block is connected to a horizontal massless spring of force co...
Text Solution
|
- A 100 g block is connected to a horizontal massless spring of force co...
Text Solution
|
- Consider the following statements about the blocks shown in the diagra...
Text Solution
|
- A simple harmonic oscillator consists of a block attached to a spring ...
Text Solution
|
- A block performs simple harmonic motion with equilibrium point x = 0 ....
Text Solution
|