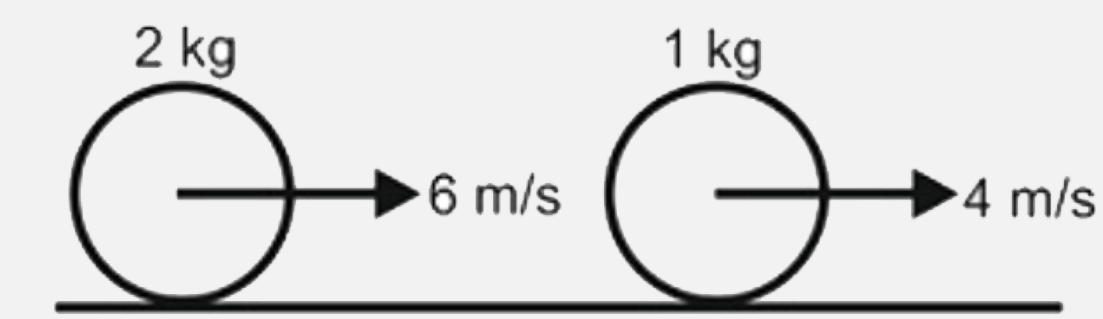
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two bodies collide as shown in the diagram. During the collision , the...
Text Solution
|
- Two balls of masses m and 2m and momenta 4p and 2p (in the directions ...
Text Solution
|
- Comprehension # 2 When two bodies collide normally they exert equal an...
Text Solution
|
- Comprehension # 2 When two bodies collide normally they exert equal ...
Text Solution
|
- A body of mass 2 kg, travelling at 4 m/s makes a head-on collision wit...
Text Solution
|
- A body of mass 5 kg starts from the origin with an intial with an inti...
Text Solution
|
- Two bodies, each having a mass of 3kg, collide with each other. One bo...
Text Solution
|
- A body .A. with a momentum .P. collides with another identical station...
Text Solution
|
- A body .A. with a momentum .P. collides with another identical station...
Text Solution
|