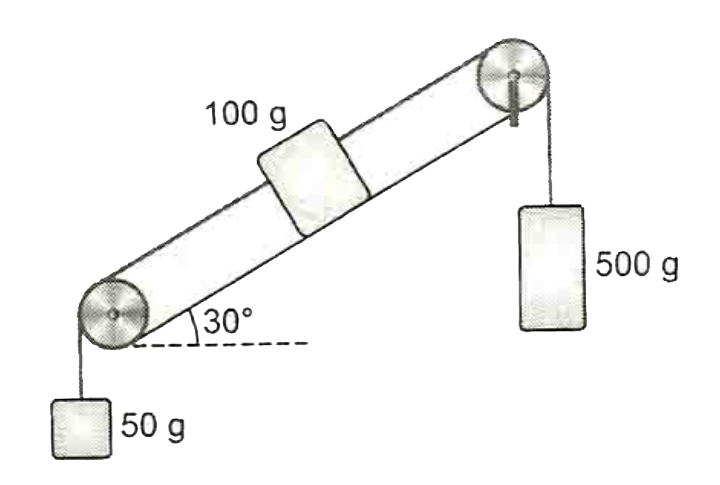
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The acceleration of the 500 g block in figure is
Text Solution
|
- In an arrangement shown in the figure, the acceleration of block A and...
Text Solution
|
- चित्र में दिखाए गए 500 g द्रव्यमान के गुटके का त्वरण ज्ञात करें |
Text Solution
|
- In the given figure , what wil be the acceleration of each block ?
Text Solution
|
- The acceleration of the 10 kg mass block shown in the figure is : -
Text Solution
|
- For the system shown in figure, the acceleration of the block is :-
Text Solution
|
- Three blocks are suspended as shown in the figure. The acceleration of...
Text Solution
|
- Find the contact force between the block and acceleration of the block...
Text Solution
|
- In the figure shown, find out acceleration of each block.
Text Solution
|