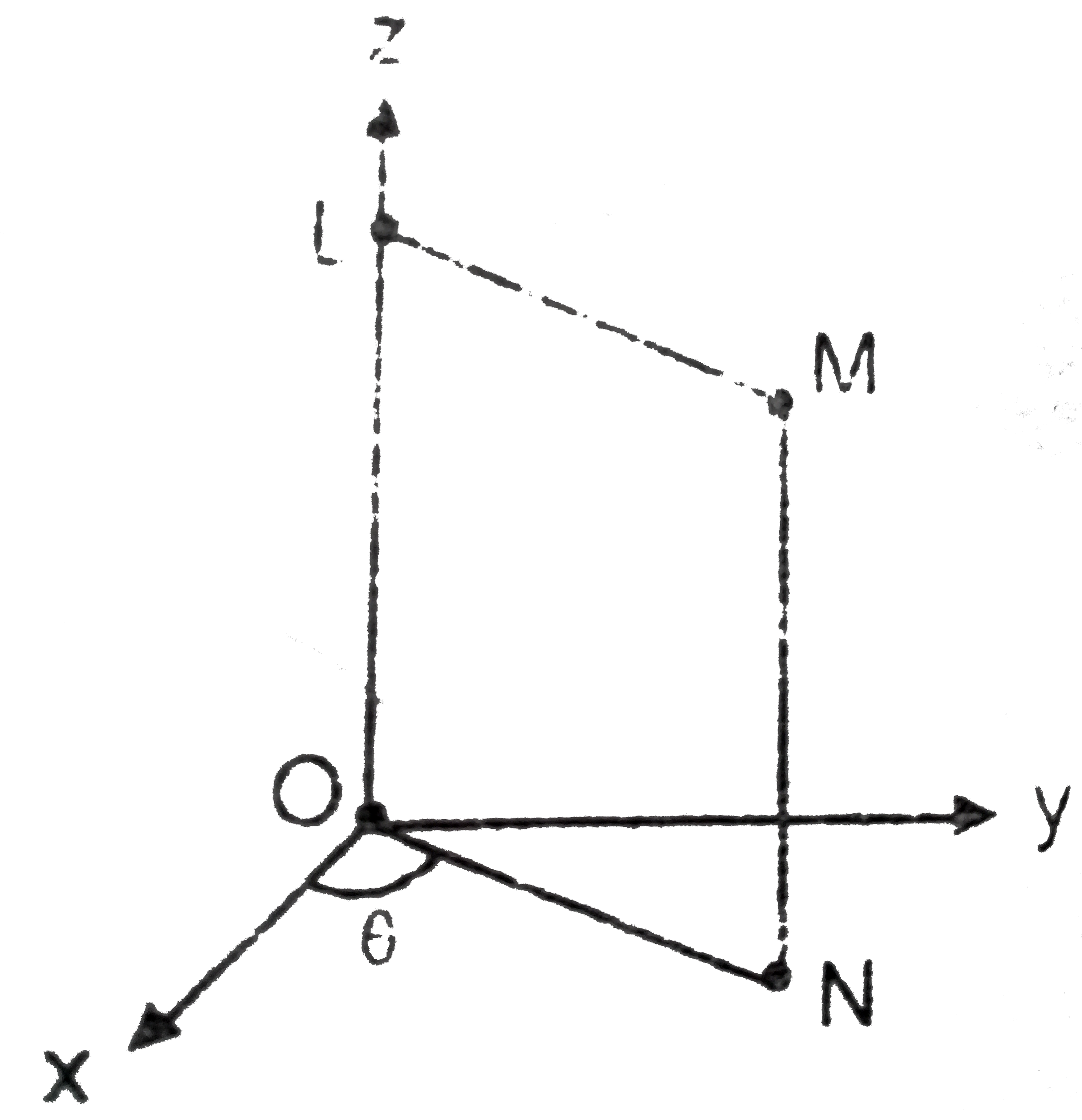
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The electric field intensity at all points in space is given by vec(E)...
Text Solution
|
- Consider a unifrom electric field vec(E) = 4xx10^(3) hat(i) NC^(-1) (i...
Text Solution
|
- Consider a uniform electric field E = 3xx10^(3) hat(i) N//C. (a) What...
Text Solution
|
- The electric field intensity at all points in space is given by vec(E)...
Text Solution
|
- The electric field intensity at all points in space is given by vec(E)...
Text Solution
|
- The electric field intensity at all points in space is given by vec(E)...
Text Solution
|
- The electric field intensity at all points in space is given by vec(E)...
Text Solution
|
- the electric field intensity at all points is space is given by vecE...
Text Solution
|
- If the electric field in a region is given by vec(E) = 5 hat(i) + 4 ha...
Text Solution
|