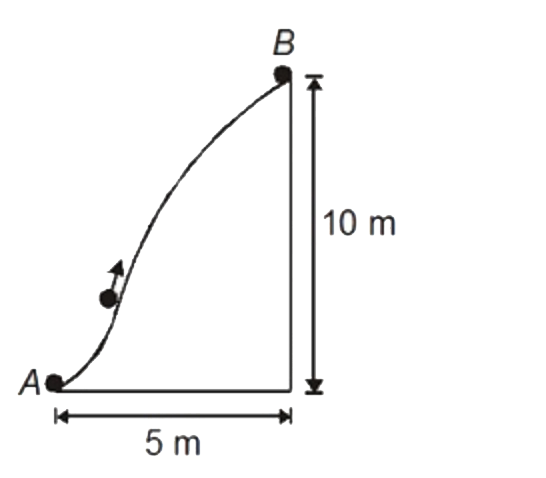
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle is pulled along a curved surface very slowly. The coefficie...
Text Solution
|
- A block of mass M is being pulley along horizontal surface .The coeffi...
Text Solution
|
- A block of mass m is slowly pulled along a curved surface from positio...
Text Solution
|
- A particle is exeuting SHM . At a point x = A//3 , kinetic energy of t...
Text Solution
|
- A particle A of mass m is situated at highest point of wedge B of mass...
Text Solution
|
- In gravity free space, a particle is in constant with the inner surfac...
Text Solution
|
- A heavy particle of mass m is in motion on a smooth surface of hemisph...
Text Solution
|
- m द्रव्यमान का एक कण r त्रिज्या के ऊर्ध्वाधर वृत्त में गतिमान है | उच्...
Text Solution
|
- A particle is pulled along a curved surface very slowly. The coefficie...
Text Solution
|