A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
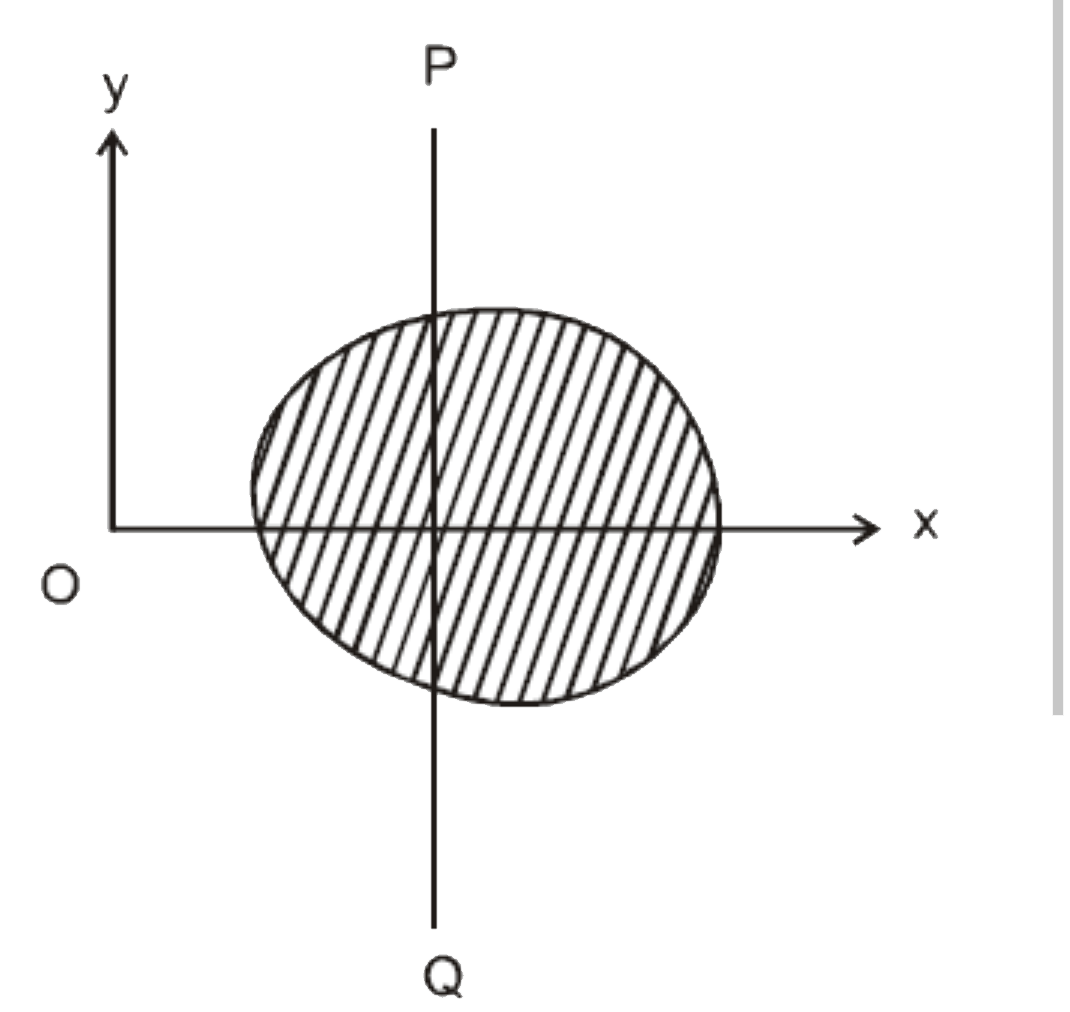
- Line PQ is parallel to y - axis and moment of inertia of a rigid body ...
Text Solution
|
- Assertion: Moment of inertia of a rigid body about any axis passing th...
Text Solution
|
- The moment of inertia of a rigid body is not unique , about a given ax...
Text Solution
|
- Minimum moment of inertia of a uniform body is I about and axis. The a...
Text Solution
|
- If I(0) is the moment of inertia body about an axis passing through it...
Text Solution
|
- यदि किसी पिण्ड का द्रव्यमान M है तथा किसी अक्ष के परितः जड़त्व-आघूर्ण I...
Text Solution
|
- जड़त्व- आघूर्ण संबंधी समान्तर अक्षों के प्रमेय का उल्लेख कीजिए तथा उसको...
Text Solution
|
- Moment of inertia of a rigid body about an axis passing through its ce...
Text Solution
|
- The moment of inertia of a ring of mass M and radius R about PQ axis w...
Text Solution
|