A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
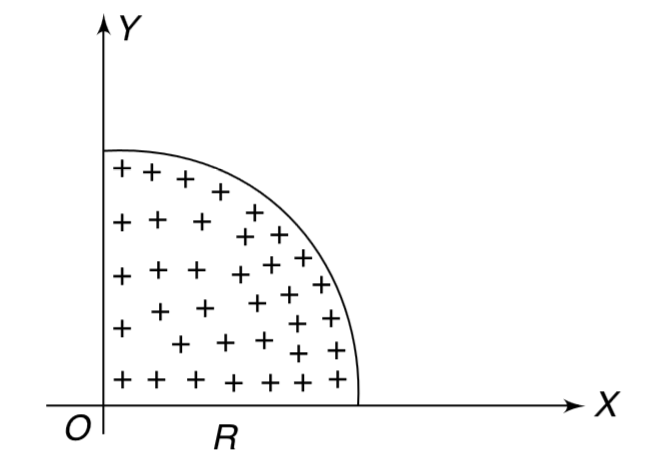
- The quarter disc of radius R (see figure) has a uniform surface charge...
Text Solution
|
- In Figure, /X=62^0,/X Y Z=54^0dot If Y O and Z O are bisectors of /X Y...
Text Solution
|
- A quarter ring of radius R is having uniform charge density lambda . F...
Text Solution
|
- A non-conducting semi circular disc (as shown in figure) has a uniform...
Text Solution
|
- The surface charge density of a thin charged disc of radius R is sigma...
Text Solution
|
- The quarter disc of radius R (see figure) has a uniform surface charge...
Text Solution
|
- A uniform surface charge of density sigma is given to a quarter of a d...
Text Solution
|
- A uniform disc of radius R is charged with a uniform surface charge de...
Text Solution
|
- A uniform surface charge of density sigma is given to a quarter of a d...
Text Solution
|