A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
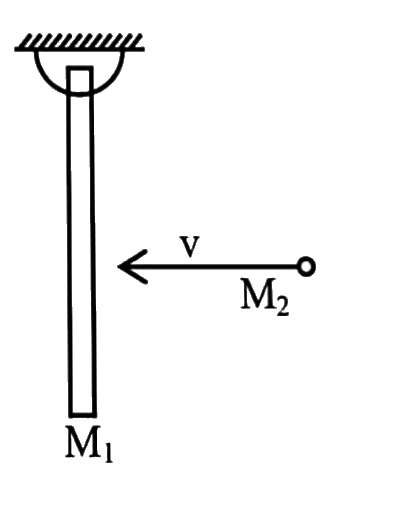
- A uniform rod of mass M(1) is hinged at its upper end as shown in the ...
Text Solution
|
- A mass m(1) moves with a great velocity. It strikes another mass m(2) ...
Text Solution
|
- A thin uniform rod of mass m and length l is kept on a smooth horizont...
Text Solution
|
- A particle of mass m(1) moving on a smooth surface with some velocity...
Text Solution
|
- A uniform rod of mass M is hinged at its upper end. A particle of mass...
Text Solution
|
- A slender rod is hinged at its top end and hanging freely in a vertica...
Text Solution
|
- A uniform rod of mass M(1) is hinged at its upper end as shown in the ...
Text Solution
|
- A particle P strikes the rod R perpendicularly as shown. The rod is su...
Text Solution
|
- A particle of mass m1 makes a head - on elastic collision with another...
Text Solution
|