Two identical containers of same emissivity containing liquids `A` & `B` art same temperature of `60^(@)` initially and densitiy `rhoA` and `rhoB` respectively. Where `rhoA lt rhoB`. Which plot best represents the temperature varitation of both with time? Given `(S_(A) = 1000(J)/(kg - K), S_(B) = 2000(J)/(kg- K))`
Two identical containers of same emissivity containing liquids `A` & `B` art same temperature of `60^(@)` initially and densitiy `rhoA` and `rhoB` respectively. Where `rhoA lt rhoB`. Which plot best represents the temperature varitation of both with time? Given `(S_(A) = 1000(J)/(kg - K), S_(B) = 2000(J)/(kg- K))`
A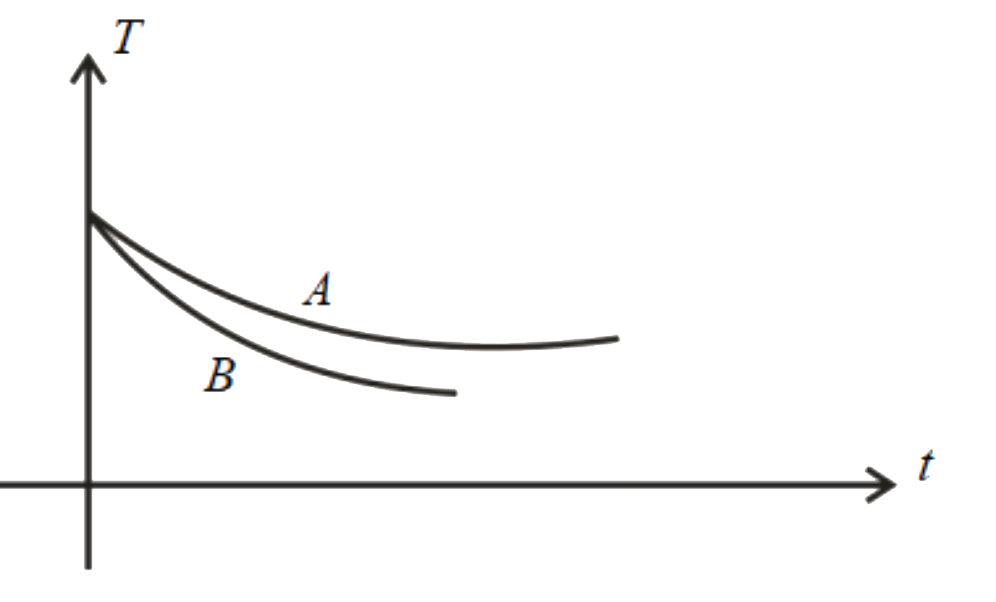

B

C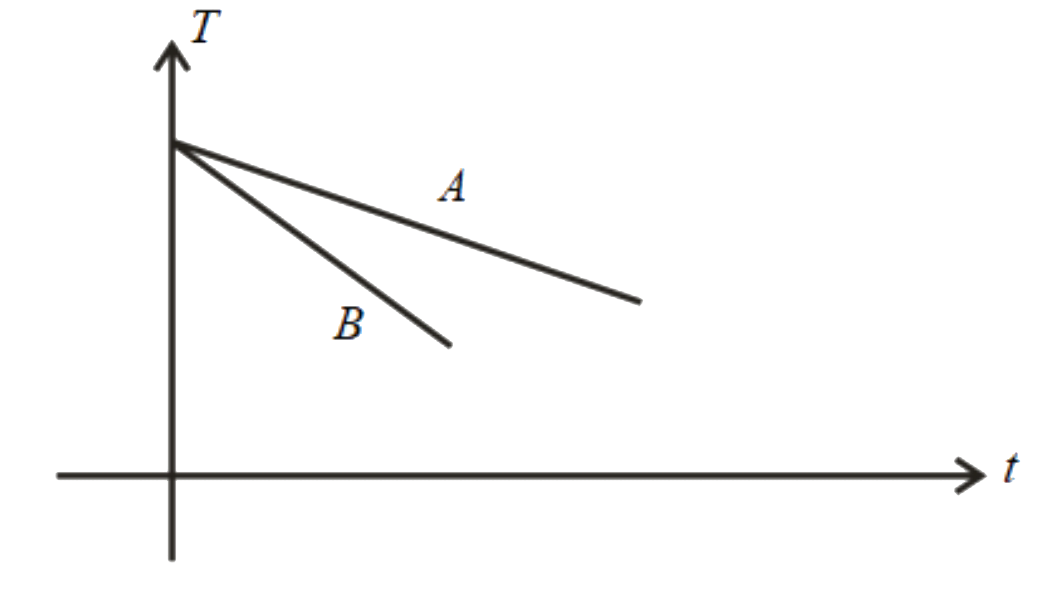

D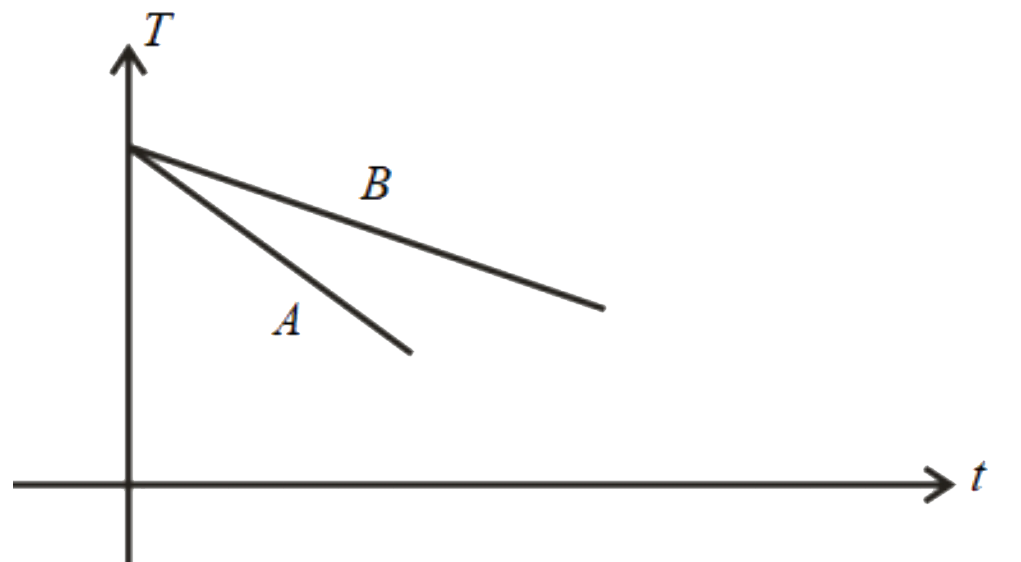

Text Solution
AI Generated Solution
The correct Answer is:
To solve the problem, we need to analyze the temperature variation of two liquids, A and B, in identical containers over time, given their specific heat capacities and densities.
### Step-by-Step Solution:
1. **Understanding the Problem**:
- We have two liquids A and B, both starting at the same temperature of 60°C.
- The specific heat capacities are given as \( S_A = 1000 \, \text{J/(kg·K)} \) and \( S_B = 2000 \, \text{J/(kg·K)} \).
- The densities are \( \rho_A < \rho_B \), which implies that the mass of liquid A is less than that of liquid B.
2. **Newton's Law of Cooling**:
- According to Newton's Law of Cooling, the rate of change of temperature of an object is proportional to the difference between its temperature and the ambient temperature.
- Mathematically, this can be expressed as:
\[
\frac{dT}{dt} = -k(T - T_0)
\]
- Where \( k \) is a constant that depends on the properties of the liquid and the environment.
3. **Finding the Mass of the Liquids**:
- The mass \( m \) of the liquids can be calculated using the formula:
\[
m = \rho \cdot V
\]
- Since the containers are identical, we can assume the volume \( V \) is the same for both liquids.
- Therefore, we have:
\[
m_A = \rho_A \cdot V \quad \text{and} \quad m_B = \rho_B \cdot V
\]
4. **Analyzing the Rate of Temperature Change**:
- The rate of temperature change can be expressed as:
\[
\frac{dT}{dt} \propto -\frac{1}{m \cdot S}
\]
- Since \( S_A < S_B \) and \( m_A < m_B \), we can conclude:
\[
\frac{dT_A}{dt} > \frac{dT_B}{dt}
\]
- This means that liquid A will cool down faster than liquid B.
5. **Graphical Representation**:
- Both liquids start at the same temperature (60°C) at \( t = 0 \).
- Since liquid A cools faster, its temperature will decrease more rapidly than that of liquid B.
- Therefore, the plot of temperature versus time will show a steeper decline for liquid A compared to liquid B.
6. **Conclusion**:
- The best representation of the temperature variation of both liquids over time will show liquid A decreasing faster than liquid B, starting from the same initial temperature.
### Final Answer:
The correct plot that represents the temperature variation of both liquids A and B with time is **option B**.
Similar Questions
Explore conceptually related problems
Two metallic spheres S_1 and S_2 are made of the same material and have got identical surface finish. The mass of S_1 is thrice that of S_2 . Both the spheres are heated to the same high temperature and placed in the same room having lower temperature but are thermally insulated from each other. the ratio of the initial rate of cooling of S_1 to that of S_2 is (a)1/3 (b)1/(sqrt3) (c) (sqrt3)/1 (d) (1/3)^(1/3)
A situation is shown in which two objects A and B start their motion from same point in same direction. The graph of their velocities against time is drawn. u_A and u_B are the initial velocities of A and B respectively. T is the time at which their velocities become equal after start of motion. You cannot use the data of one question while solving another question of the same set. So all the questions are independent of each other. 7. After 10 s of the start of motion of both objects A and B, find the value of velocity of A if u_A = 6 ms^-1 , u_B = 12 ms^-1 and at T velocity of A is 8 ms^-1 and T = 4s
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100 J//kg-K , specific heat of water =4200 J//kg-K , and latent heat of fusion of ice =3.3xx10^5 J//kg . Initial mass of the ice in the container equal to
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100 J//kg-K , specific heat of water =4200 J//kg-K , and latent heat of fusion of ice =3.3xx10^5 J//kg . Initial mass of the ice in the container equal to
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100 J//kg-K , specific heat of water =4200 J//kg-K , and latent heat of fusion of ice =3.3xx10^5 J//kg .
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100 J//kg-K , specific heat of water =4200 J//kg-K , and latent heat of fusion of ice =3.3xx10^5 J//kg . The value of rate P is?
The system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at TK . Standard vapour pressures of A and B are P_(A)^(0) and P_(B)^(0) , respectively, at TK . We collect the vapour of A and B in two containers of volume V , first container is maintained at 2 T K and second container is maintained at 3T//2 . At the temperature greater than T K , both A and B exist in only gaseous form. We assume than collected gases behave ideally at 2 T K and there may take place an isomerisation reaction in which A gets converted into B by first-order kinetics reaction given as: Aoverset(k)rarrB , where k is a rate constant. In container ( II ) at the given temperature 3T//2 , A and B are ideal in nature and non reacting in nature. A small pin hole is made into container. We can determine the initial rate of effusion of both gases in vacuum by the expression r=K.(P)/(sqrt(M_(0))) where P= pressure differences between system and surrounding K= positive constant M_(0)= molecular weight of the gas If vapours are collected in a container of volume 8.21 L maintained at 3 T//2K , where T=50 K , then the ratio of initial rate of effusion of gases A and B is given as
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100 J//kg-K , specific heat of water =4200 J//kg-K , and latent heat of fusion of ice =3.3xx10^5 J//kg . The mass of the ice formed due to conversion from the water till thermal equilibrium is reached is equal to
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100 J//kg-K , specific heat of water =4200 J//kg-K , and latent heat of fusion of ice =3.3xx10^5 J//kg . The mass of the ice formed due to conversion from the water till thermal equilibrium is reached is equal to
Two closed Identical conducting containers are found in the laboratory of an old scientist. For the verification of the gas some experiments are performed on the two boxes and the results are noted. Experiment 1 When the two containers are weighed W_(A) = 225g , W_(B) = 160g and mass of evacuated container W_(C) = 100g . Experiment 2. when the two containers are given same amount of heat same temperature rise is recorded . The pressure change found are DeltaP_(A) = 2.5"atm" . " " DeltaP_(B) = 1.5"atm" Identify the type of gas filled in container A and B respectively
Recommended Questions
- Two identical containers of same emissivity containing liquids A & B a...
Text Solution
|
- Two identical containers of same emissivity containing liquids A & B a...
Text Solution
|
- In a insulated vessel, 0.05 kg steam at 373 K and 0.45 kg of ice at 25...
Text Solution
|
- A calorimeter of mass 0.2 kg and specific heat 900 J//kg-K . Containin...
Text Solution
|
- 30 gram copper is heated to increase its temperature by 20^@ C if the ...
Text Solution
|
- 0.3 Kg of hot coffee, which is at 70^(@)C , is poured into a cup of ma...
Text Solution
|
- When 1.5 kg of ice at 0^(@)C mixed with 2 kg of water at 70^(@)C in a ...
Text Solution
|
- Two identical beakers A and B contain equal volumes of two different l...
Text Solution
|
- Two bodies A and B of same mass, area and surface finish with specific...
Text Solution
|