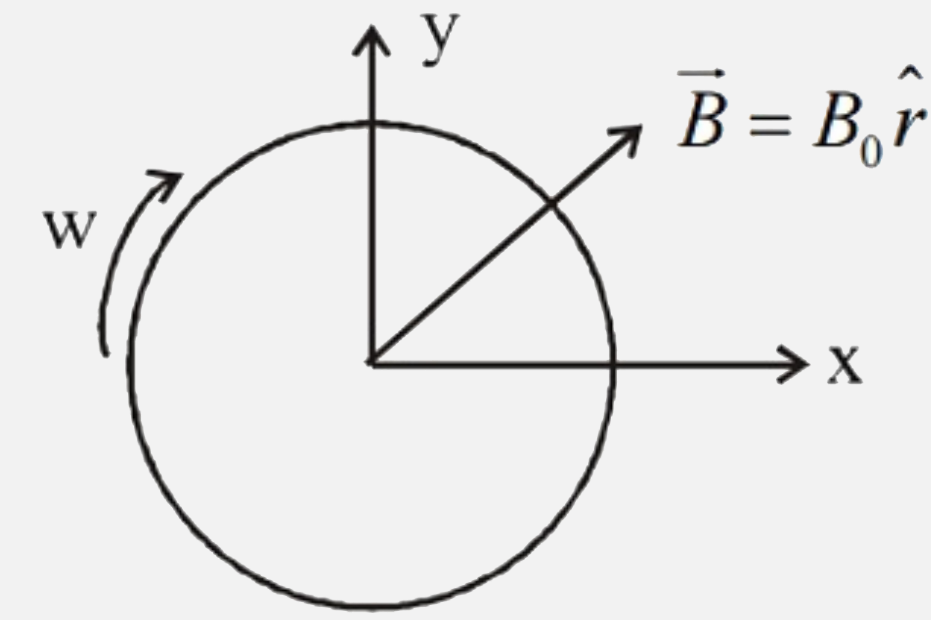
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A thin non conducting disc of mass M = 2 kg, charge Q = 2 xx 10^(2-) C...
Text Solution
|
- The electric field in a region is radially outward with magnitude E = ...
Text Solution
|
- A line charge lambda per unit length is pasted uniformly on to the wir...
Text Solution
|
- A uniform magnetic field vec(B) = 3 hat i + 4 hat j + hat k exists in ...
Text Solution
|
- If the work required to move the conductor shown in figure, one full t...
Text Solution
|
- In region x gt 0 a uniform and constant magnetic field vec(B)(1) = 2 B...
Text Solution
|
- A time varying uniform magnetic field passes through a circular region...
Text Solution
|
- In a right handed coordinate system XY plane is horizontal and Z-axis ...
Text Solution
|
- In a region of space, magnetic field exists in a cylindrical region of...
Text Solution
|