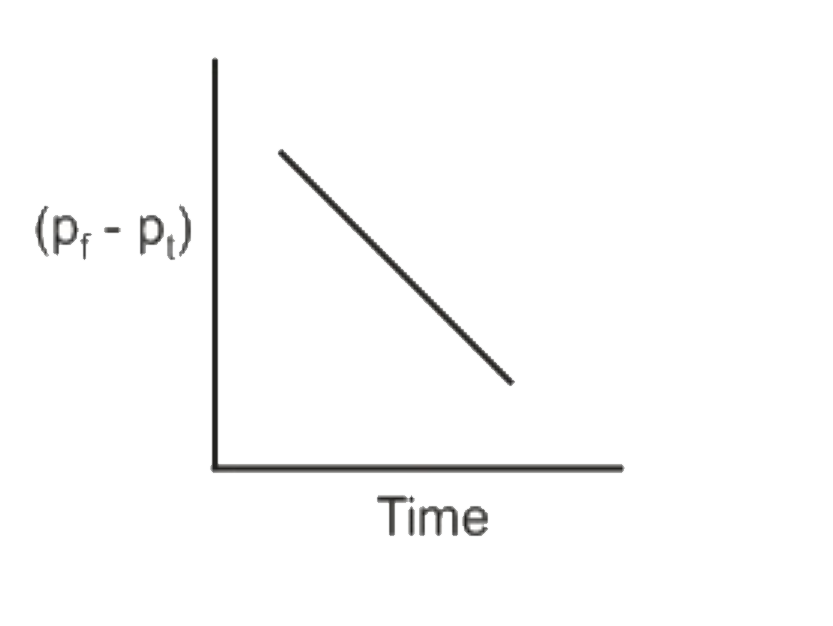
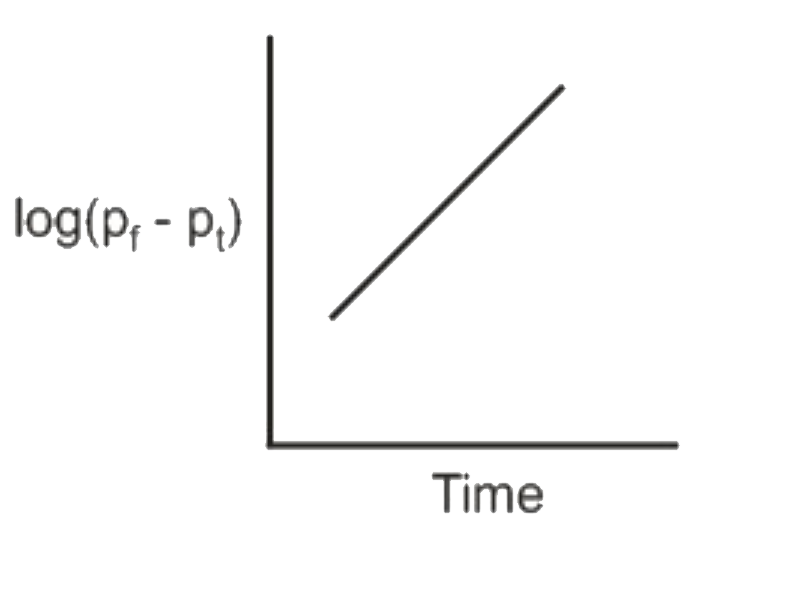
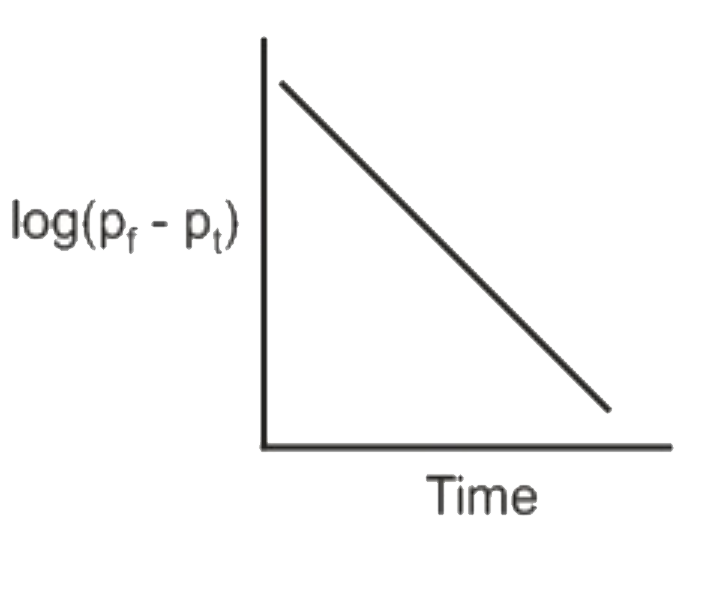
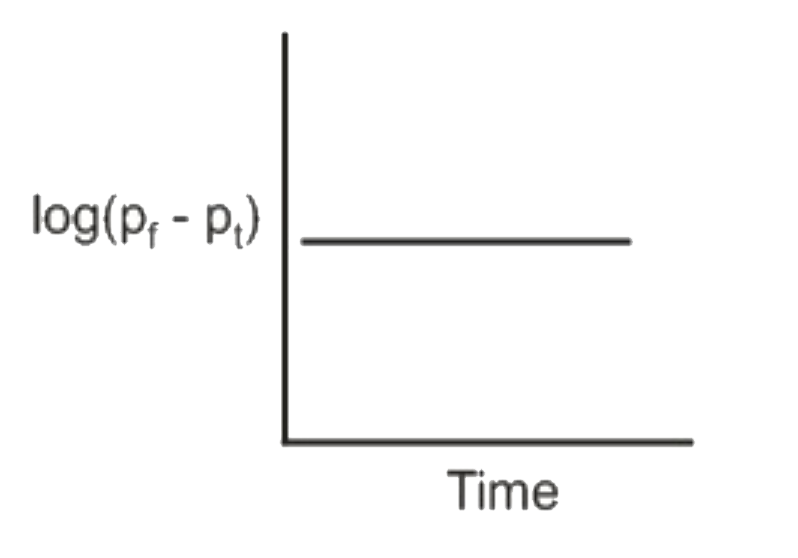
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Benene diazonium chloride in aqueous solution decomposes as : C6H5-N=N...
Text Solution
|
- Identify the oxidant the reductant in the following reaction. Cl(2)(g)...
Text Solution
|
- The reaction Cl(2(g)) + 2 I((aq))^(-) to 2 Cl((aq))^(-) + I(2(s)) In t...
Text Solution
|
- निम्नलिखित रेडॉक्स अभिक्रिया को सन्तुलित कीजिए - Cl(2) + OH^(-)toCl^...
Text Solution
|
- Benene diaxonium chloride in aqeous solution decomposes as : C6H5-N=N^...
Text Solution
|
- Let us consider the following two reaction. 2NaCl((aq))+F(2(g))to2NaF(...
Text Solution
|
- The following reaction follows first order kinetics : C6H5 - N = N^(+)...
Text Solution
|
- What volume of 0.250 M HNO3 reacts with 42.4 mL of 0.150 M Na2CO3 in t...
Text Solution
|
- What volume of 0.250 M HNO3 reacts with 42.4 mL of 0.150 M Na2CO3 in t...
Text Solution
|