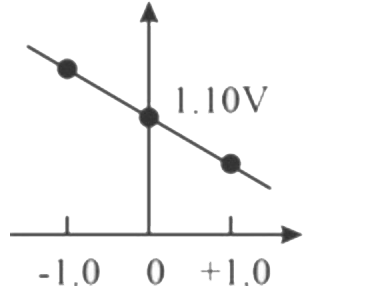
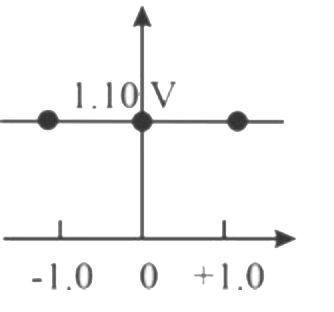
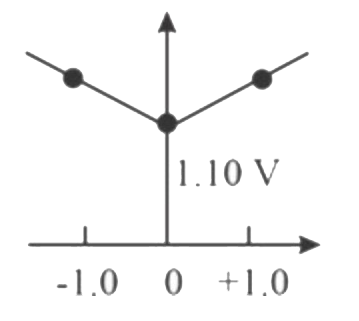
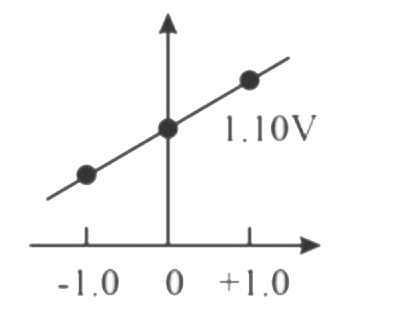A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Which graph correctly correlates E("cell") as a function of concentrat...
Text Solution
|
- A graph is plotted between E(cell) and log .([Zn^(2+)])/([Cu^(2+)]) . ...
Text Solution
|
- Which graph correctly correlates E(cell) as a funcation of concentrati...
Text Solution
|
- Which graph correctly correlates E(cell) as a function of concentratio...
Text Solution
|
- The cell, Zn//Zn^(2+)(1M)"//"Cu^(2+)(1M)//Cu(E(cell)^(@)=1.10V) , was ...
Text Solution
|
- For a standard cell Zn(s)|Zn^(2+)(1 M)||Cu^(2+)(1 M)|Cu(s) Write the e...
Text Solution
|
- For the redox process Zn (s) + Cu^(2+) hArr Zn^(2+) + Cu(s) E("cell")^...
Text Solution
|
- The standard cell potential for the cell Zn|Zn^(2+) (1 M)|| Cu^(2+) (1...
Text Solution
|
- Which graph correctly correlates E("cell") as a function of concentrat...
Text Solution
|