A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
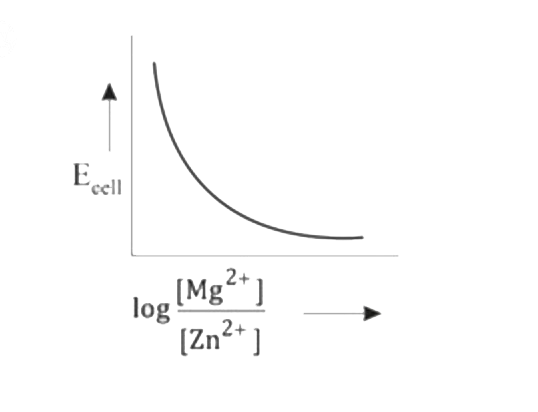
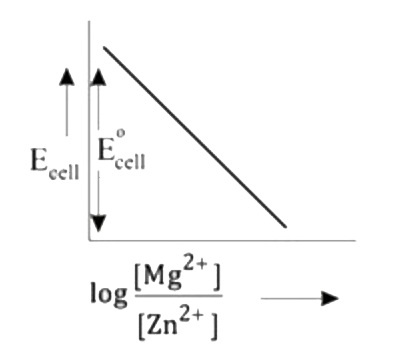
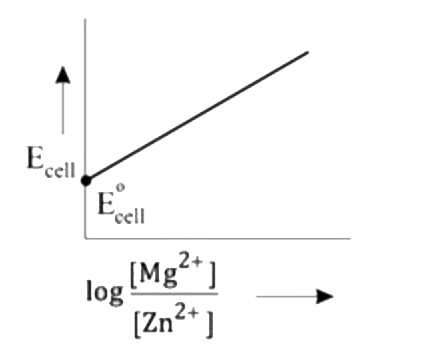
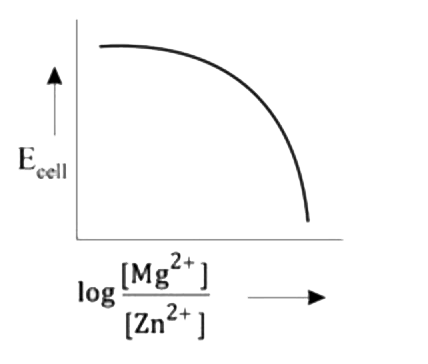
- Mg(s)|Mg^(2+)(aq)||Zn^(2+)(aq)|Zn(s),E^(@)=+3.13V The correct plot o...
Text Solution
|
- Each of the following redox reaction occurs spontaneously. Mg(s)+Zn^...
Text Solution
|
- Mg(s)|Mg^(2+)(aq)||Zn^(2+)(aq)|Zn(s),E^(@)=+3.13V The correct plot o...
Text Solution
|
- Write the cell reaction for the electrochemical cell represented as Zn...
Text Solution
|
- सेल अभिक्रिया के साथ सेल के लिए DeltarG^@, Zn(s) + Ag2O(s) + H2O(l) ...
Text Solution
|
- For the galvanic cell Mg(s)|Mg^(2+)(aq)||Zn^(2+)(aq)|Zn(s),the standar...
Text Solution
|
- For the cell reaction Zn(s)+Mg^(2+) (1M)=Zn^(2+) (1M) +Mg , the emf ha...
Text Solution
|
- For the galvanic cell Mg(s)|Mg^(2+)(aq)||Zn^(2+)(aq)|Zn(s) ,the standa...
Text Solution
|
- Mg(s)|Mg^(2+)(aq)||Zn^(2+)(aq)|Zn(s),E^(@)=+3.13V The correct plot of ...
Text Solution
|