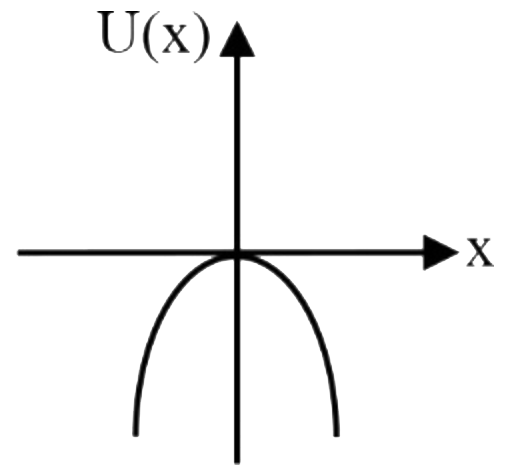
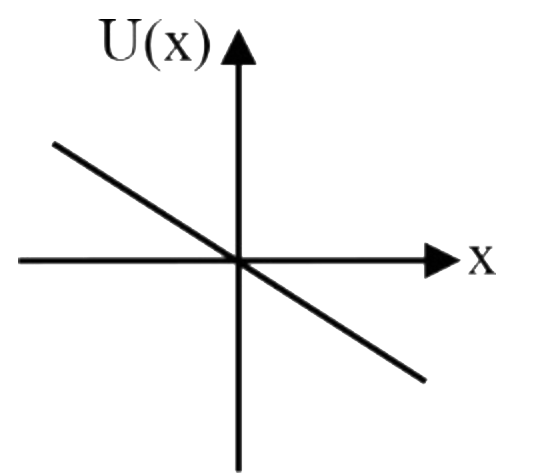
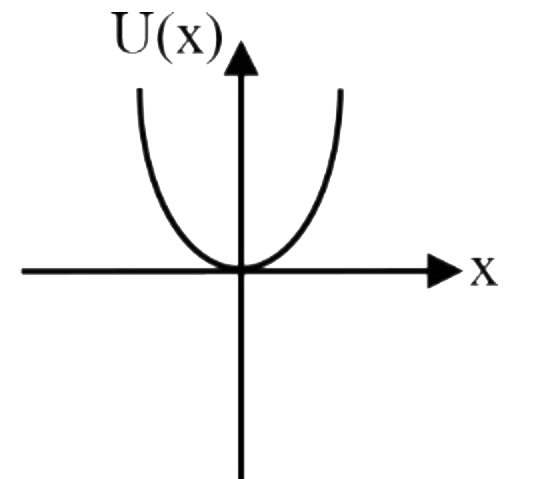
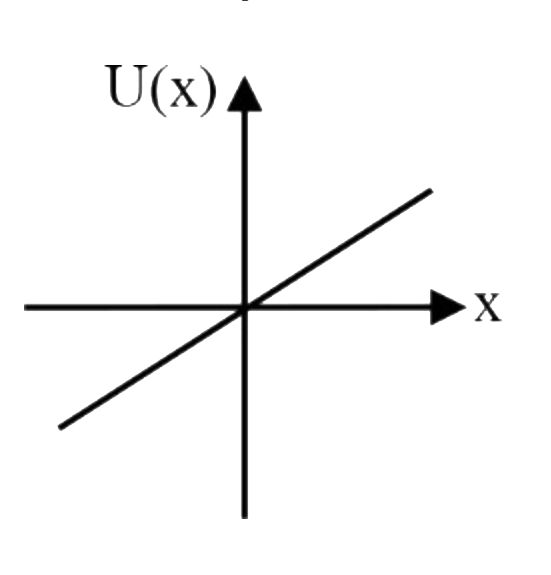
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle is placed at the origin and a force F=Kx is acting on it (w...
Text Solution
|
- A particle is placed at the origin and a force F=Kx is acting on it (w...
Text Solution
|
- A particle, which is constrained to move along the x-axis, is subjecte...
Text Solution
|
- On a particle placed at origin a variable force F=-ax(where a is a pos...
Text Solution
|
- A particle is placed at the origin and a force F = kx is acting on it ...
Text Solution
|
- एक कण मूल बिंदु पर स्थित है तथा इस पर बल F =kx (k धनात्मक नियतनाक है ...
Text Solution
|
- A particle is placed at the origin and a force F = kx is acting on it ...
Text Solution
|
- A particle is placed at the origin and a force F = kx is acting on it ...
Text Solution
|
- A particle is placed at the origin and a force F=Kx is acting on it (w...
Text Solution
|