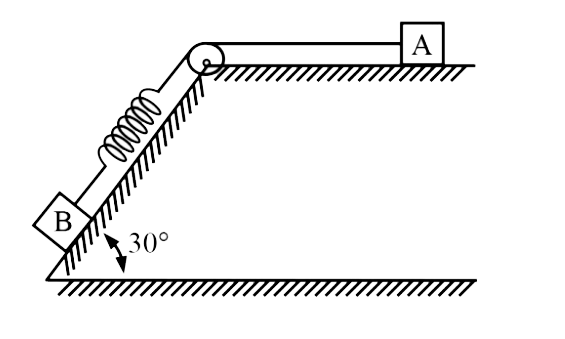
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A massless string and a spring connect two blocks A and B to each othe...
Text Solution
|
- Two blocksA andB are connected to each other by a string and a spring ...
Text Solution
|
- A block of mass m is moving with a speed v on a horizontal rough surfa...
Text Solution
|
- Two blocks A and B are connected to each other by a string and a sprin...
Text Solution
|
- Two block of same mass'm' are joined with an dideal spring of spring c...
Text Solution
|
- Two blocks A and B are connected to each other by a string and a sprin...
Text Solution
|
- Two block of masses M and m are connected to each other by a massless ...
Text Solution
|
- A massless string and a spring connect two blocks A and B to each othe...
Text Solution
|
- Two blocks A and B are connected to each other by a string and spring ...
Text Solution
|