A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
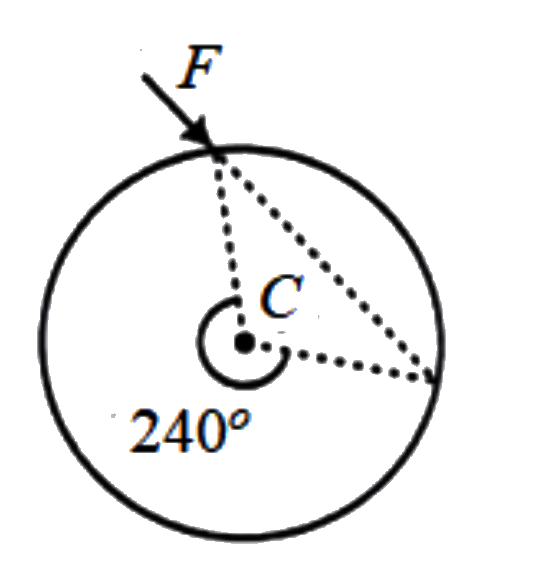
- A uniform disc of mass M and radius R is hinged at its centre C . A fo...
Text Solution
|
- A disc of mass M and radius R can rotate freely in a vertical plane ab...
Text Solution
|
- A force F acts tangentially on a part of a uniform disc of mass 'm' an...
Text Solution
|
- A disc of mass m and radius R is placed over a plank of same mass m. T...
Text Solution
|
- A disc of mass m and radius R is placed over a plank of same mass m. T...
Text Solution
|
- Two equal and opposite forces are allplied tangentially to a uniform d...
Text Solution
|
- A disc of mass M and radius R moves in the x-y plane as shown in the f...
Text Solution
|
- A uniform disc of mass M and radius R is hinged at its centre C . A fo...
Text Solution
|
- A uniform disc of mass M and radius R is hinged at its centre C. A for...
Text Solution
|