A
B
C
D
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
AGRAWAL PUBLICATION-SAMPLE PAPER 10-EXERCISE
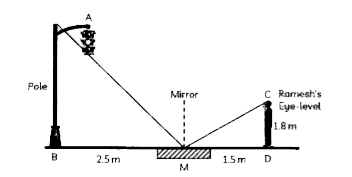
- Ramesh places a mirror on level ground to determine the height of a po...
Text Solution
|
- Ramesh places a mirror on level ground to determine the height of a po...
Text Solution
|
- Ramesh places a mirror on level ground to determine the height of a po...
Text Solution
|
- Ramesh places a mirror on level ground to determine the height of a po...
Text Solution
|
- Ramesh places a mirror on level ground to determine the height of a po...
Text Solution
|
- 4 boys are having a night in and one of the boy's mother decides to pl...
Text Solution
|
- 4 boys are having a night in and one of the boy's mother decides to pl...
Text Solution
|
- 4 boys are having a night in and one of the boy's mother decides to pl...
Text Solution
|
- Using prime factorisation, find the LCM of 90 and 120.
Text Solution
|
- Using the quadratic formula, find the roots of the quadratic equation:...
Text Solution
|
- If tan A = (7)/(24) find the value of sin A cos A.
Text Solution
|
- Prove that sin^(2) A+ sin^(2) A tan^(2) A = tan^(2) A .
Text Solution
|
- If the centroid of Delta ABC having vertices A(a, b), B(b, c) and C(c,...
Text Solution
|
- The perimeter of a sheet of paper in the shape of a quadrant of a circ...
Text Solution
|
- If sin theta + cos theta = sqrt 3, then what is tan theta + cot thet...
Text Solution
|
- Evaluate : (sin 30^(@) + tan45^(@) - cosec 60^(@))/(sec 30^(@) + cos 6...
Text Solution
|
- If the points A(1,-2),B(2,3),C(a,2)andD(-4,-3) forms a parallelogram, ...
Text Solution
|
- In the figure, all three sides of a triangle ABC touch the circle at p...
Text Solution
|
- The product of the LCM and HCF of two numbers is 24.The difference of ...
Text Solution
|
- How many spherical lead shots each 4.2 cm in diameter can be obtain...
Text Solution
|