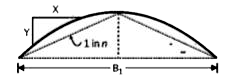
A
B
C
D
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
AGRAWAL PUBLICATION-SAMPLE PAPER 1-EXERCISE
- Case Study Based- 3 Applications of Parabolas-Highway Overpasses/Und...
Text Solution
|
- Case Study Based- 3 Applications of Parabolas-Highway Overpasses/Und...
Text Solution
|
- Case Study Based- 3 Applications of Parabolas-Highway Overpasses/Und...
Text Solution
|
- Case Study Based- 4 100m RACE A stopwatch was used to find the time...
Text Solution
|
- Case Study Based- 4 100m RACE A stopwatch was used to find the tim...
Text Solution
|
- Case Study Based- 4 100m RACE A stopwatch was used to find the tim...
Text Solution
|
- Case Study Based- 4 100m RACE A stopwatch was used to find the tim...
Text Solution
|
- Case Study Based- 4 100m RACE A stopwatch was used to find the tim...
Text Solution
|
- 3 bells ring at an interval of 4,7 and 14 minutes. All three bell rang...
Text Solution
|
- Find the point on x-axis which is equidistant from the points (2,-2) a...
Text Solution
|
- Find the point on x-axis which is equidistant from the points (2,-2) a...
Text Solution
|
- Find a quadratic polynomial whose zeroes are 5-3sqrt(2 )and 5+3sqrt(2)...
Text Solution
|
- Draw a line segment AB of length 9cm. With A and B as centres, draw ci...
Text Solution
|
- If sqrt(3)sintheta-costheta=sqrt(2), then one general value of theta i...
Text Solution
|
- In the figure, quadrilateral ABCD is circumscribing a circle with cent...
Text Solution
|
- Prove that2-sqrt3 is irrational.
Text Solution
|
- The roots alpha and beta of the quadratic equation x^(2) - 5x + 3(k-1)...
Text Solution
|
- In the figure, ABCD is a square of side 14 cm. Semi-circles are drawn ...
Text Solution
|
- The perimeters of two similar triangles are 25 cm and 15 cm respective...
Text Solution
|
- In an equilateral triangle ABC, D is a point on side BC such that B D=...
Text Solution
|