Ramesh places a mirror on level ground t...

Ramesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively.

If the distance of Ramesh and the pole from the mirror are 2.5 m and 1.5 m respectively, then the height of the pole is:

3 metres

2.1 metres

1.8 metres

1.08 metres

Text Solution

Verified by Experts

Topper's Solved these Questions

2020 QUESTION PAPER (1)
AGRAWAL PUBLICATION|Exercise EXERCISE|33 Videos

Similar Questions

Explore conceptually related problems

Ramesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively. The height of the pole is:

Ramesh places a mirror on level ground to determine the height of a pole (with traffic light fired on it) (see the figure). He stands at a certain distance so that he can see the top of the pole reflected from the mirror. Ramesh's eye level is 1.8 m above the ground. The distance of Ramesh and the pole from the mirror are 1.5 m and 2.5 m respectively. The height of the pole is:

Anjali places a mirror on level ground to determine the height of a tree (see the diagram) . She stands at a certain distance so that she can see the top of the tree reflected from the mirror . Anjali's eye level is 1.8 m above the ground . The distance of Anjali and the tree from the mirror are 1.5 m and 2.5 m respectively. (i) Name the two similar triangles that are formed in the diagram. ii. State the criterion of similarity that is applicable here. iii. Find the height of the trees.

An object is placed at 20 cm from a convex mirror of focal length 20 cm. The distance of the image from the pole of the mirror is

AGRAWAL PUBLICATION-(2019) QUESTION PAPER-EXAMPLE

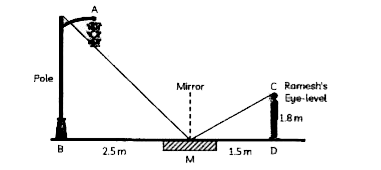
Ramesh places a mirror on level ground to determine the height of a po...
Text Solution
|
Check whether g(x) is a factor of P(x) by dividing polynomial p(x) by ...
Text Solution
|
Find the area of the triangle formed by joining the mid-points of the ...
Text Solution
|
Draw the graph of the equations x-y+ 1 = 0 and 3x + 2y - 12 = 0. Using...
Text Solution
|
Prove that sqrt 3 is an irrational number.
Text Solution
|
Find the greatest number which on dividing 1251, 9377 and 15628 leaves...
Text Solution
|
A,B and C are interior angles of a triangle ABC. Show that sin[(B+C)/2...
Text Solution
|
If angle A = 90^@, then find the value of tan [(B + C)/2]
Text Solution
|
If tan(A +B) = 1 and tan(A - B) = 1/ sqrt 3, 0^@ < A + B < 90^@, A>B, ...
Text Solution
|
In Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. Th...
Text Solution
|
Prove that opposite sides of a quadrilateral circumscribing a circel s...
Text Solution
|
Water in a canal, 6 m wide an 1.5 m deep, is flowing with a speed of 1...
Text Solution
|
A class teacher has the following absentee record of 40 students of a ...
Text Solution
|
A car has two wipers which do not overlap. Each wiper has a blade of l...
Text Solution
|
A pole has to be erected at a point on the boundary of a circular park...
Text Solution
|
If m times the m^(th) term of an Arithmetic Progession is equal to n t...
Text Solution
|
The sum of the first three numbers is an Arithmetic Progression is 18....
Text Solution
|
Construct a triangle ABC with side BC = 6 cm, AB = 5 cm and angle ABC ...
Text Solution
|
In Figure, a decorative block is shown which is made of two solids, a ...
Text Solution
|
In Figure, a decorative block is shown which is made of two solids, a ...
Text Solution
|
A bucket open at the top is in the form of a frustum of a cone with a ...
Text Solution
|