Similar Questions
Explore conceptually related problems
Recommended Questions
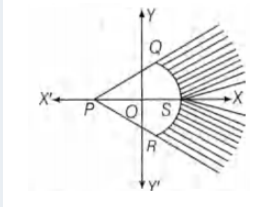
- The shaded region, where P=(-1,0),Q=(-1+sqrt(2),sqrt(2))R=(-1+sqrt(2),...
Text Solution
|
- let z= (-1+sqrt(3i))/2, where i=sqrt(-1) and r,s epsilon P1,2,3}. Let ...
Text Solution
|
- If e^(x)=(sqrt(1+z)-sqrt(1-z))/(sqrt(1+z)+sqrt(1-z)) and tan (y/2)=sq...
Text Solution
|
- If log sqrt(3)((|z|^(2)-|z|+1)/(2+|z|))gt2, then the locus of z is
Text Solution
|
- Let z = (-1 + sqrt(3i))/(2) , where i= sqrt(-1) , and r,s in {1,2,3}...
Text Solution
|
- If |z|=1 and w=(z-1)/(z+1) (where z!=-1), then R e(w) is 0 (b) 1/(|...
Text Solution
|
- For |z-1|=1, show that tan{[a r g(z-1)]/2}-((2i)/z)=-i
Text Solution
|
- If |z-2-i|=|z|sin(pi/4-a r g z)| , where i=sqrt(-1) ,then locus of z,...
Text Solution
|
- let z= (-1+sqrt(3i))/2, where i=sqrt(-1) and r,s epsilon P1,2,3}. Let ...
Text Solution
|