Similar Questions
Explore conceptually related problems
Recommended Questions
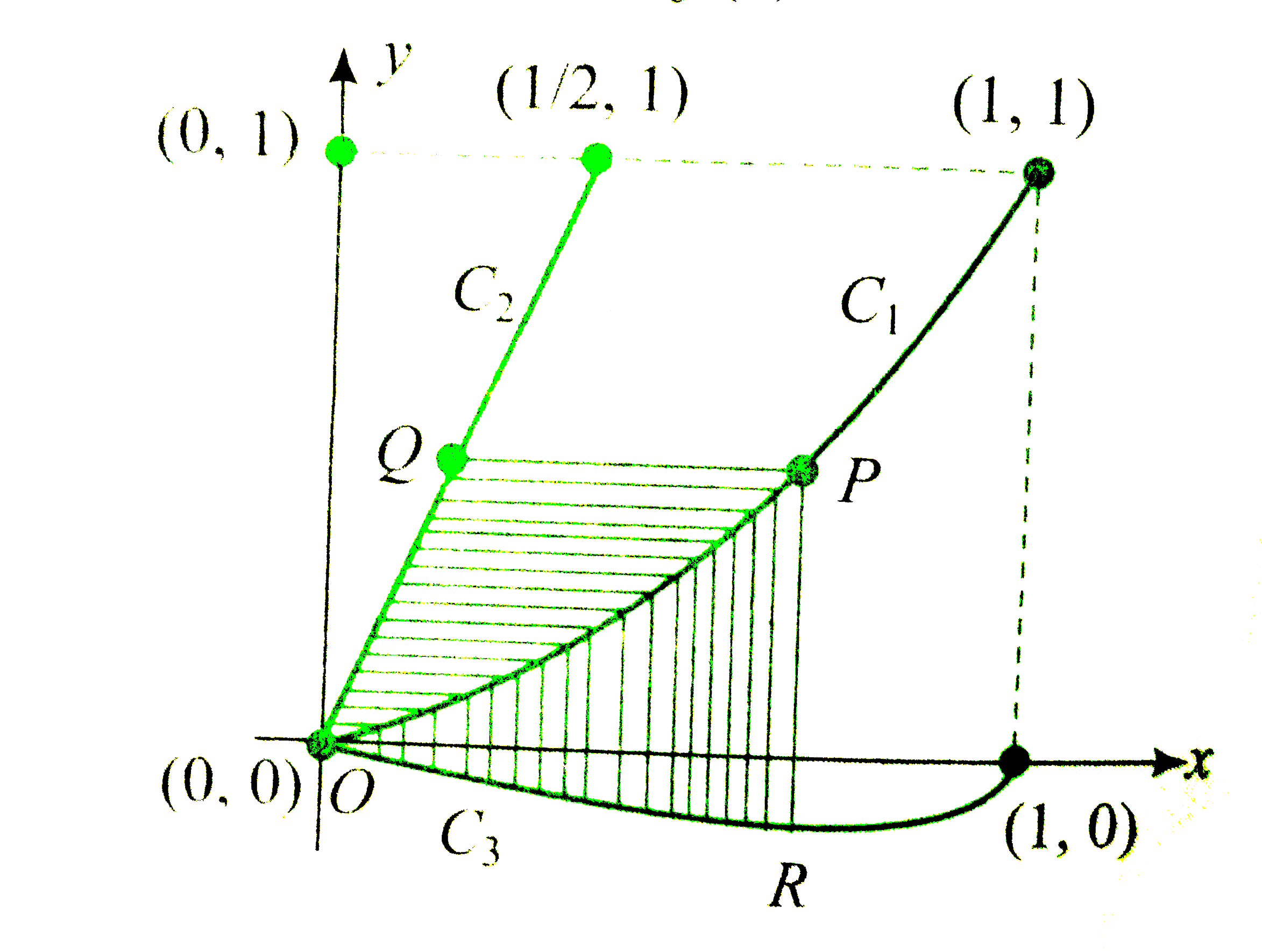
- Let C(1) and C(2) be the graphs of the functions y=x^(2) and y=2x, res...
Text Solution
|
- Let C(1) and C(2) be the graphs of the functions y=x^(2) and y=2x, res...
Text Solution
|
- Evaluate |{:(.^(x)C(1),,.^(x)C(2),,.^(x)C(3)),(.^(y)C(1),,.^(y)C(2),,....
Text Solution
|
- Let C(1) and C(2) denote the centres of the circles x^(2) +y^(2)...
Text Solution
|
- Let n be a positive integer and (1+x)^(n)+C(0)+C(1)x+C(2)x^(2)+C(3)x...
Text Solution
|
- If f(x) is a differentiable function wherever it is continuous and f'(...
Text Solution
|
- If f(x) is a differentiable function wherever it is continuous and f'(...
Text Solution
|
- If f(x) is a differentiable function wherever it is continuous and f'(...
Text Solution
|
- माना C(1) और C(2) क्रमशः फलन y=x^(2) औरy=2x, 0 le x le 1 के ग्राफ...
Text Solution
|